皆さんが自宅を出発して帰宅するまでの経路を地図に描くと平面上の曲線ができあがります.

この軌跡上の点は数学的には時刻 \( t \) をパラメータとする関数 \( x(t),y(t) \) を使って \( (x(t),y(t)) \) と表せるもので,曲線は
\[ C=\{ ( x ( t ) , y ( t ) ) | a \leqq t \leqq b\} \]となります.上の絵のような端のないものは閉曲線とよばれています.これから閉曲線の特徴が数学的にどのようにして捉えるのかを説明しましょう.まず曲線に角があれば,それは目立った特徴といえるでしょう.

このような角を通過するときは経験的に必ずそこで止まる必要が あります.これは速度ベクトル \( (x'(t),y'(t)) \) が \( t=t_0 \) において \( 0 \) ということを意味してます.この対偶をとると任意の時刻 \( t \) において \( (x'(t),y'(t))\neq 0 \) をみたす閉曲線は角がないです.この条件をみたすものを正則曲線といいます.
角がない正則曲線にはどんな特徴があるのでしょうか.速度ベクトル \( (x'(t),y'(t)) \) は長さと方向を持っていますが,それぞれは極座標表示
\[ (x(t),y(t)) = (r(t) \cos \theta (t),r (t) \sin \theta (t)) \]を使うと \( r (t), \theta (t) \) によって表されます.
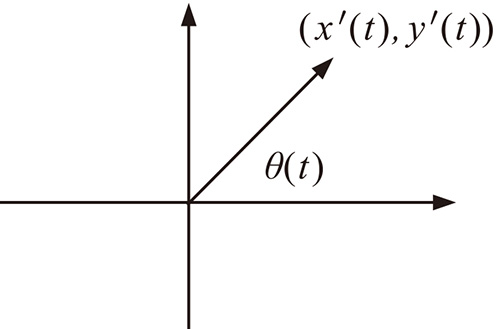
\( r (t) \)は速度ベクトルの長さ,つまり速さであって,
\( r(t) = \sqrt{x'(t)^2 + y'(t)^2} \) と書かれます.速さを積分すると曲線 \( C \)の長さが得られます.それを\( l(C) \) と書くと
となることはご存知でしょう.
一方,速度ベクトルの向き \( \theta (t) \) は時刻 \( t \) における進む向きです.したがって,進む向きが変化していることが \( \theta (t) \) の変化によってわかります.例えば, \( \theta (t) \) が \( 2\pi \) 増えることは,反時計回りに向きが一周したことを意味し, \( \theta (b) - \theta (a) \) は始点から終点までに自分が回った量を表しています.平面図形の言葉で述べると,これは曲線 \( C \) が平面上何周回った図形であるかを表していて, \( C \) の回転数とよばれています.
曲線の長さと同様に回転数を \( x (t), y (t) \) から得られる関数の積分を使っても書き表すことができます.簡単な計算から
であることがわかるので,曲線 \( C \) の回転数を \( n(C) \) と書くと
\[ n(C) = \frac{1}{2\pi}\int_{a}^{b}\frac{x'(t)y''(t)-x''(t)y'(t)}{x'(t)^2+y'(t)^2}dt \]となります.
曲線 \( C \) の長さ \( l(C) \) と回転数 \( n(C) \) は共に積分で書くことができる量として似た性質をもっています.例えば, 曲線 を平行移動したり,回転したりしても変化しません.形が変わらないことから明らかですが,式を使っても示すことができます.
しかし, \( l(C) \) と \( n(C) \) は違った性質も持っています. \( C \) を少しだけ変化させてみると, \( l(C) \) は少しだけ変化しますが, \( n(C) \) は全く変化しません.なぜなら \( n(C) \) は整数であって,少しだけ変化させることができないからです.もっと驚くべきことに,回転数が等しい二つの閉曲線は途中で角が現れないように少しずつ変化させていくとお互いに移り合うのです.これはホイットニーの定理とよばれています.以下の問を解くことによってこれを実感してください.
以下の二つの閉曲線を反時計周りに一周すると共に回転数が \( 1 \) です.
右から左に途中で角が現れないように変形してください.
