『自然現象は方程式で記述されます』と言われたら皆さんはどう思いますか?風でざわめく森の木々や、波打ち際でしぶきを上げて砕ける波を見ていると、その細部では非常に複雑な挙動をしていることが分かります。しかし、その現象の裏に潜んでいる基本原理を見い出し、それを数学の言葉で表すことにより方程式が得られます。自然現象を記述する方程式の多くは微分方程式になります。
日常よく見られる自然現象として、波および拡散などがあります。水と空気との境界面である水面は波を説明する好材料でしょう。また、音は空気の振動が波として伝わることによって伝播されます。一方、熱いお茶をそのままにしておくと室温まで温度は下がりますし、煙草の煙は空気中に広がって見えなくなってしまいますが、これらは拡散と呼ばれる現象になります。このような自然現象は誰でも知っていることですが、それらを定量的に調べようとすると偏微分方程式を使うことになります。例えば、水面の運動を考えましょう。
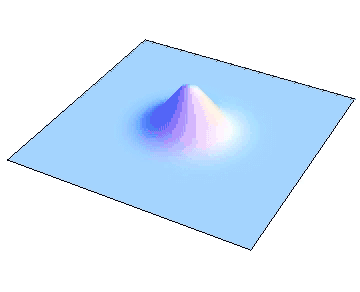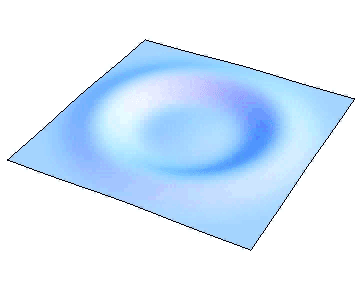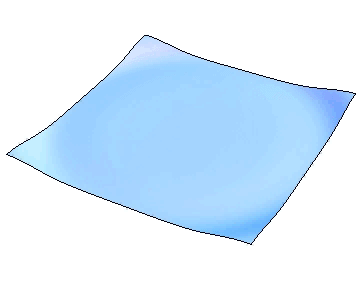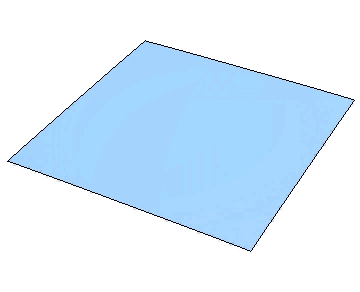
時刻 \(t\) における水面が \(z = u(x,y,t)\) というグラフで書けている場合、基本原理から従う方程式は水の波の方程式と呼ばれています。その方程式を理想化・単純化することにより波動方程式
\[ \frac{\partial^2 u}{\partial t^2} = gh\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right) \]が導かれます。ここで、 \(g\) は重力加速度、 \(h\) は平均水深です。この方程式を使えば、水面の波の伝播速度は \( \sqrt{gh} \) であることが分かります。太平洋の平均水深はおよそ \( 4[km] \) ですから、\( g=9.8[m/s^2] \) に注意してその伝播速度を計算すると、 \( \sqrt{gh} \simeq 713[km/h]\) となります。これより、太平洋を伝播する津波の速さはジェット機に匹敵ことが分かります。このように、この波動方程式でも津波の到達時間を計算するだけなら十分実用的ですが、波が崩れることや1834年にScott Russellが発見した有名な孤立波などの説明はできません。方程式を理想化・単純化する際に非線形効果を無視してしまったためです。
上の波動方程式は無限個の解をもちます。そのような解の中から2つの解 \( u_1(x,y,t),u_2(x,y,t)\) をとり、\( c_1,c_2 \) を定数として一次結合 \( c_1u_1(x,y,t)+c_2u_2(x,y,t) \) を作ると、これも解になります。このような性質は線形性と呼ばれ、線形性をもつ方程式を線形方程式、もたない方程式を非線形方程式と呼びます。
自然現象をより精密に記述する偏微分方程式はどれも非線形方程式になっています。非線形現象の一つを説明する最も単純な非線形偏微分方程式としてHopf 方程式
\[ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x}=0 \]があります。下の図は、時刻 \( t=0 \) において初期波形をあたえHopf方程式を数値的に解き、時刻 \( t = 0,0.4,0.8,1.2 \) の時の波形 \( u=U(x,t) \) を \( xu \) 平面に描いたものです。
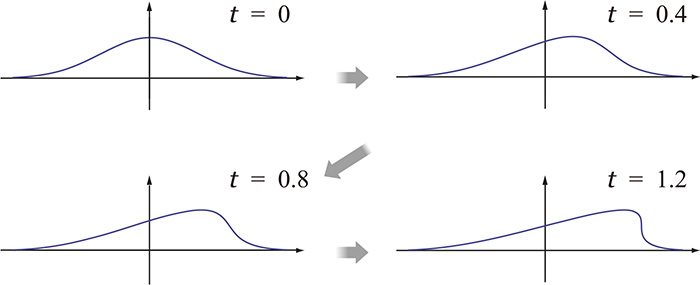
時間の経過とともに波形の右側が急峻になっていくのが見てとれます。さらに時刻\( t=1.2 \)の直ぐ直後には急峻になっている部分が不連続になり、微分方程式は意味をもたなくなってしまいます。このような現象は線形方程式では起こりません。
有限時間で方程式は意味を失っても現象は起こり続けています。したがって、Hopf方程式が現象を正しく記述していないと考えることができます。実際、Hopf方程式の導出過程では、熱の拡散と同様な機構である粘性を無視しています。それを考慮した方程式としてBurgers方程式
\[ \frac{\partial u}{\partial t} +u \frac{\partial u}{\partial x}=\mu\frac{\partial^2 u }{\partial x^2} \]があります。ここで、 \( \mu \) は正定数です。この方程式の解は、その波形が急峻になったとしても決して不連続にはならず、その解は存在し続けます。一方、Hopf 方程式の解の不連続性は、気体力学における衝撃波との関連から、物理的な意味をもちます。それを数学で表現するためには、不連続関数に対しても何らかの意味で微分を定義する必要があります。そこで登場するのが、関数の概念を拡張した超関数です。超関数として方程式の解を扱えば、Hopf 方程式で生じた困難は克服されます。この超関数の理論は数理科学科3年生向けの講義で紹介されます。
このように偏微分方程式の研究は現象の解析と密接に関連しており、数理科学を代表する学問の一つです。