降水量の一般化分散

概要

ここでは，「内測平均，分散」をもちいたデータの幾何学的特性を反映して新しく提案された統計量の計算方法を説明する．データについては，イギリスの降雨量データ，関連手法としては「内測平均，分散」を参照されたい．ここでは次節で定める\(\alpha\)距離の計算と一般化分散の計算を行う．次に，イギリスの降雨量データを9次元から3次元に圧縮するために主成分分析を行い，第1，第2，第3主成分得点を採用する．最後に，パラメータ\(\alpha\)の値，時間軸の違いによる計算結果を図示する．

\(\alpha\)距離，\(\beta\)距離，一般化平均・分散

「内測平均，分散」で説明されているように，距離空間\((M,d)\)上のデータ\(x_1,\dots,x_n\)に関する内測平均（Fréchet平均）は，以下のように定義される．

内測平均（Frechet平均）および対応する２通りの分散 \[ \begin{aligned} \hat \mu = {\rm arg}\min_{x\in M} \sum_{i=1}^n d(x_i, x)^2.\\ V^{(1)} = \frac{1}{n}\min_{x\in M} \sum_{i=1}^n d(x_i, x)^2.\\ V^{(2)} = \frac{1}{2n^2}\sum_{i=1}^n \sum_{j=1}^n d(x_i, x_j)^2 \end{aligned} \]

ここで，\((M,d)\)がユークリッド空間であるときは，\(\hat\mu\)は標本平均\(\bar{X}:=\frac{1}{n}\sum_{i=1}^n X_i\)と一致し，\(V^{(1)},V^{(2)}\)はともに標本分散\(\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2\)と一致する．ただし，一般には一般的に内測平均は一意ではなく，また\(V^{(1)}\)と\(V^{(2)}\)も一致しないため，注意が必要である．

次に，\(\alpha\)距離と一般化平均，一般化分散を定義する．本節で紹介する距離，分散についての詳しい議論については，[Kobayashi and Wynn(2014)]を参照されたい．なお，\(\alpha\)距離自体は任意の測地距離空間に定義可能であるが，ここでは簡単のため距離グラフの場合のみ説明する．距離グラフ（各辺に長さが定義されているグラフ）の各頂点間に，\(\alpha\)距離を以下のように定義する．ここで\(v, v'\)はグラフの頂点であり，\(\Gamma(v,v')\)は\(v\)と\(v'\)を結ぶグラフ上の全経路の集合とする．

\(\alpha\)距離実数\(\alpha\)に対して， \[ \begin{aligned} d_{\alpha} (v, v') & := \min_{\gamma \in \Gamma(v,v')} \sum_{e \in \gamma} |e|^{1-\alpha}. \\ \end{aligned} \]

ただし，\(|e|\)は経路\(\gamma\)上の辺\(e\)の長さである．\(\alpha=0\)のときは，単にグラフ上の最短経路長と一致する．

各頂点がデータ点に対応しているような距離グラフのことを経験グラフとよぶ．ここでは完全グラフを考え，データ\(x_i\)と\(x_j\)に対応する２頂点\(v_i\)と\(v_j\)を結ぶ辺の長さはデータ点間の距離\(\|x_i-x_j\|\)で与えられているものとする．このとき，\(\alpha\)距離を用いた経験グラフ上の一般化平均，分散を次のように定める．ただし，グラフの全頂点集合を\(V\)とする．

\(\alpha\)距離に基づく一般化平均および２通りの一般化分散 \[ \begin{aligned} \hat \mu_{\alpha} = {\rm arg}\min_{v \in V} \sum_{i=1}^n d_\alpha (v_i, v)^2 \\ V_{\alpha}^{(1)} = \frac{1}{n} \min_{v \in V} \sum_{i=1}^n d_\alpha(v_i, v)^2 \\ V_{\alpha}^{(2)} = \frac{1}{2n^2}\sum_{i=1}^n \sum_{j=1}^n d_\alpha(v_i, v_j)^2 \end{aligned} \]

Rによる計算と考察

計算については，著者が作成した関数を利用する．関連するRのスクリプトファイルは「C1_floyd.cpp」「C2_dPathLengthAb.R」，「C3_path.calc.R」，「C4_UK.plot3d.R」である．ここでは，2011年のデータについて計算を行っていく．まずは，イギリスの降雨量データのダウンロードとデータの整形を行う．ダウンロードについてR上で行わず，直接ブラウザより行いたい方については，(ダウンロードページ)からダウンロードをしてほしい．

              
                # download file name and object name
                dfn <- c("SEEP", "SWEP", "CEP", "NWEP", "NEEP", "SSP", "NSP", "ESP", "NIP")

                # set working directory
                cd_path <- "please set path of working space"

                # create foloder for download data named "dataset"
                if(!"dataset" %in% list.files(cd_path)){
                  dir.create(file.path(cd_path, "dataset"))
                }

                # a directory to save download files
                dfolder_path <- file.path(cd_path, "dataset")

                # list class object for data
                Data_list <- list()

                # downloading and importing data
                for(i in 1:length(dfn)){
                  # file link
                  txt_url <- paste("https://www.metoffice.gov.uk/hadobs/hadukp/data/daily/Had", dfn[i], "_daily_qc.txt", sep="")

                  # download path
                  txt_DLname <- file.path(dfolder_path, paste(dfn[i], "txt", sep="."))

                  # downloading
                  download.file(txt_url, txt_DLname)

                  # importing
                  tmp <- read.table(file=txt_DLname, skip=3)
                  Data_list[[i]] <- tmp[{tmp$V1>=1931}&{tmp$V1<=2015}, ]

                  # adding a name
                  names(Data_list)[i] <- dfn[i]
                }

                # a day doesn't exist in leap year
                omit_leap <- c(61,62,124,186,279,341)

                # a day doesn't exist in non leap year
                omit_nonleap  <- c(60,61,62,124,186,279,341)

                # leap year list
                leap_year <- 1932 + seq(0, 4*21, 4)

                # creating datetime matrix "ymd"
                day   <- rep(1:31, 12)
                month <- rep(1:12, each=31)

                for(yy in 1931:2015){ ## START FOR yy
                  if(yy==1931){ ## START IF 1
                      md  <- data.frame(month=month, day=day)
                      ymd <- data.frame(year=yy, md)
                  }else{ ## ELSE IF 1
                      md  <- data.frame(month=month, day=day)
                      ymd <- rbind(ymd, data.frame(year=yy, md))
                  } ## END IF 1
                } ## END FOR yy

                # creating rainfall data matrix "rain_data"
                rain_data <- sapply(Data_list, FUN=function(l){
                  as.vector(t(l[,-c(1,2)]))
                })

                # merging datetime and rainfall data "rain_uk"
                rain_uk <- data.frame(ymd, rain_data)[,-1]

次に，自作関数path.calcを用いて\(\alpha\)距離の計算を行う．計算にあたっては，あらかじめdplyrとRcppをインストールしておいてほしい．

              
                # パッケージと関数を読み込み
                library(dplyr)
                library(Rcpp)
                source("C1_floyd.cpp")
                source("C2_dPathLengthAb.R")
                source("C3_path.calc.R")

                # 2011年のデータに対して計算を行う
                result <- path.calc(AllData=rain_uk, year=2011, alphas=-1))

                # 3dプロット
                UK.plot3d(result)

次に，3次元での測地部分グラフの可視化を行う(図１，図２)．測地部分グラフとは，全頂点ペアを結ぶ測地線（最短経路）で用いられる辺だけを残して作られる部分グラフであり，一般化平均や分散の計算にはこの部分グラフのみの情報が用いられる．path.calc関数の中では，Xp要素に主成分分析によって3次元に次元削減を行った結果を格納している．UK.plot3d関数ではこの次元削減した点を用いて図示している．

\(\alpha = 0\)

\(\alpha = -1\)

              
                library(rgl)
                source("C4_UK.plot3d.R")

                # rglのplot3dを用いて図示
                UK.plot3d(result)

続いて，一般化分散について図示する(図３，図４)．path.calc関数の結果の中のSPL_listには２種類の分散の計算結果が保存されている．これらはそれぞれ，距離行列の要素の平均と，列和の最小値として計算されており，上記の\(V_\alpha^{(1)}\)および\(2V_\alpha^{(2)}\)に対応する．ここでは，各年についての分散を計算し系列プロットとして図示する．

              
                # 1931 ~ 2015年まで各年で計算を行う
                res_var <- data.frame(year=1931:2015, sum=NA, min=NA)
                for(yy in 1:nrow(res_var)){
                  res_var[yy,-1] <- path.calc(AllData=rain_uk, year=res_var$year[yy], alpha=-1)$SPL_list[[1]]
                  print(yy)
                }

                # 図示
                matplot(x=res_var$year, res_var[,-1], type="l", lty=1, xlab="year", ylab="variance")

図３：\(\alpha = -1\)の場合の一般化分散の比較

図４：\(\alpha = 0\)の場合の一般化分散の比較

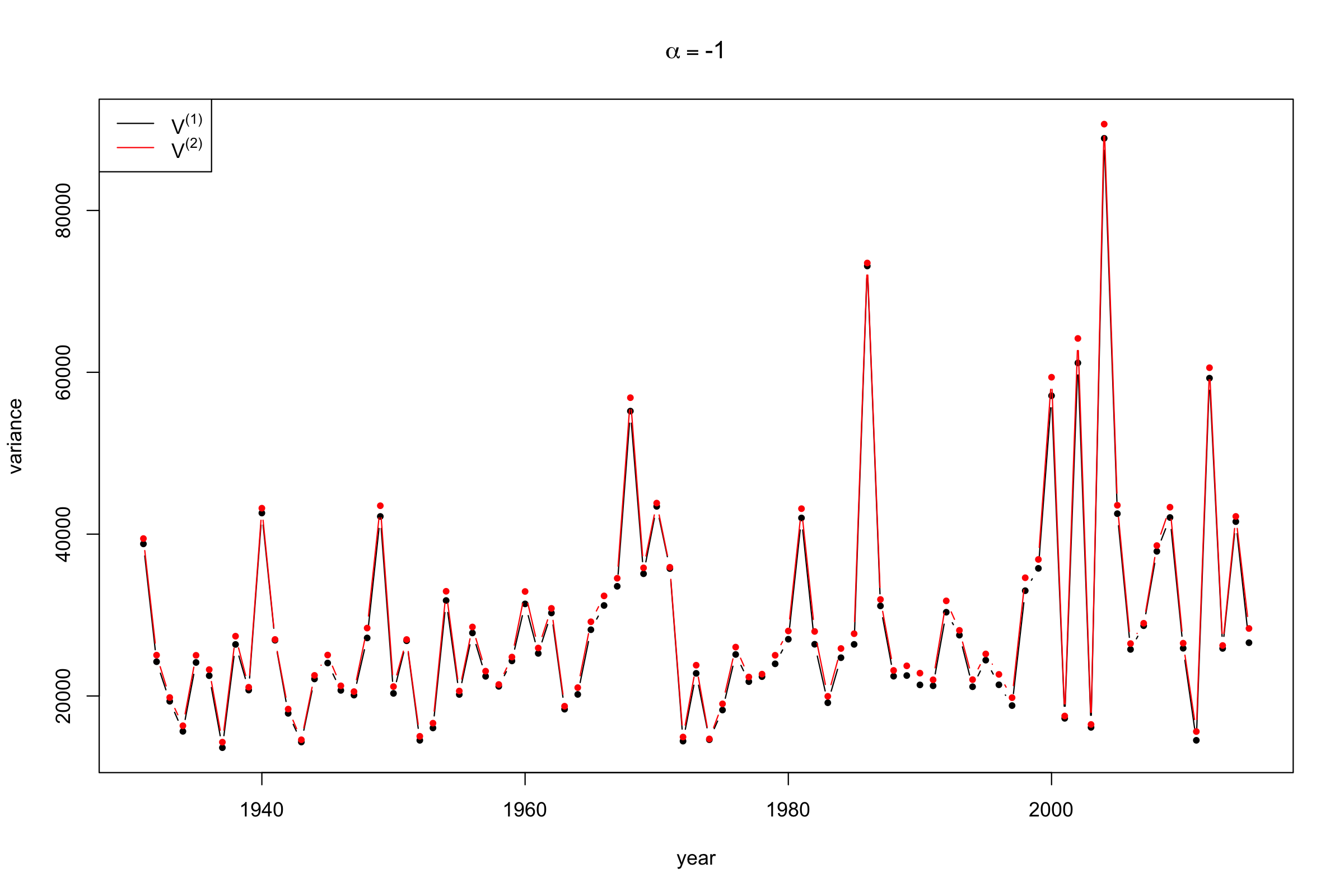
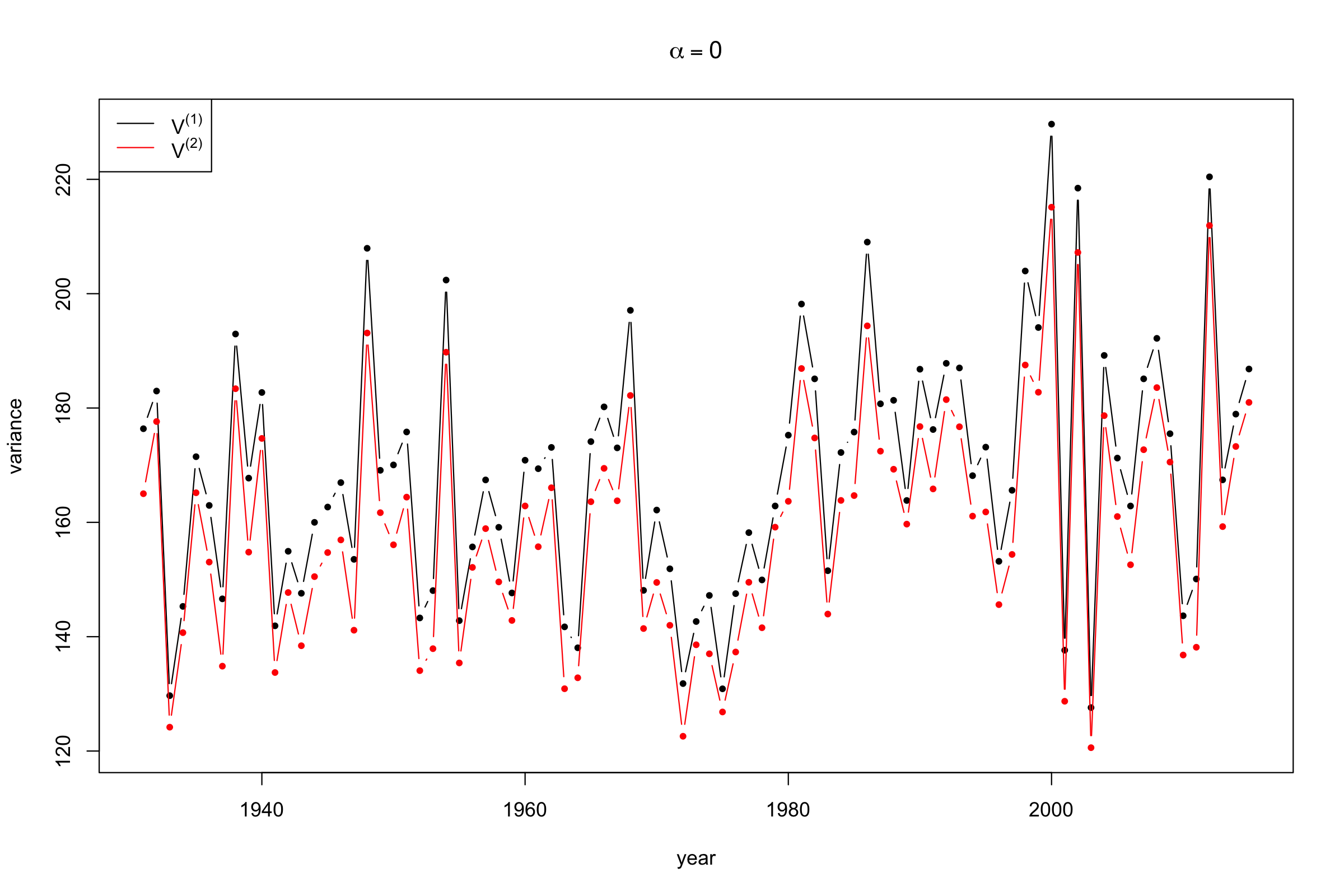
\(\alpha\)の値や計算する年数を変化させた場合の分散の可視化についてはこちらのページを参照されたい．このページはshinyパッケージを用いて作成した．
図３，図４をみると2000年あたりで分散がもっとも大きい値を取っていることがわかる．

【参考文献】
Kei Kobayashi, Henry P. Wynn (2014), Empirical geodesic graphs and CAT(k) metrics for data analysis, arXiv1401.3020