主成分分析
概要
ここでは,主成分分析を紹介する.主成分分析はデータが持つ情報を要約する手法と捉えることができる.本Webサイトのイギリスの降雨量に関する解析に用いている.その際,9地区の降雨量は9次元データであり,これを3次元に縮約するために主成分分析を利用している.ここでいう「情報」とは分散を意味しており,まずデータ空間に対して直交行列による座標変換を施す.このとき,分散が大きい方向順に軸を考え,大きい方から第1主成分,第2主成分,・・・としていくことになる.特に,相関を持つデータは主成分ごとに分散の大きさが異なるので,分散が大きい主成分に注目することにより,
情報の損失を抑えつつデータの次元を削減することが可能となる.
気象データの解析においては,イギリスの降雨量においては全体に主成分分析を用いて次元削減を行なっており, また年間の日付ごとのデータにおいても主成分分析を行いある日付における特徴の可視化のために用いている.
主成分
いま,\(p\)次元ベクトルとしてデータが\(n\)対与えられているとする.つまり,\(\boldsymbol x_1, \boldsymbol x_2, \ldots, \boldsymbol x_n\)が 与えられていて,これに対して標本平均ベクトルを\( \bar{\boldsymbol{x}} = \frac{1}{n} \sum_{i=1}^{n} \boldsymbol x_i \)とする. ここでは,あらかじめ各観測項目において平均0,分散1となるように基準化したものとする. 利用するデータによっては,変数間でスケールの違いが大きいことがあり,主成分分析の結果にスケールの違いが大きく影響することがある. そのような場合は基準化したデータを用いた方が解釈がしやすくなるため,主成分分析を行う前にはデータのスケールを確認した方が良い. 次に,標本分散共分散行列を\(S\)とする.ここで,\(S\)の\((ij)\)成分は\(\boldsymbol x_i\)と\(\boldsymbol x_j\)の標本共分散\({\rm Cov}(\boldsymbol x_i, \boldsymbol x_j)\)であり, 特に\((i,i)\)成分は\(\boldsymbol x_i\)の標本分散\( {\rm Var}(\boldsymbol x_i) \)である.共分散・分散の定義を示す.
ここで,\( \bar{\boldsymbol x}_i\)はベクトル\(\boldsymbol x_i\)の平均ベクトルである.分散共分散行列は半正定値性を持つことが示され(ここに参考文献を入れる) そのため固有値は全て非負の値を持つという性質を持つ. このとき,\(S\)の固有値を大きい順に\( (\lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_p)\)とし, それぞれの固有値に対応するノルム1で互いに直交する固有ベクトルを\( \boldsymbol \alpha_1, \boldsymbol \alpha_2, \ldots, \boldsymbol \alpha_p \)とする. ここでデータ\(\boldsymbol x_i\)の第1主成分得点は,標本分散共分散行列\(S\)の最大固有値\(\lambda_1\)に対するノルム\(1\)の固有ベクトル\(\boldsymbol \alpha_1 \)を用いた 次のような内積である.
ここで\(i=1,\ldots,n\)であり,このとき第1主成分の標本分散は最大固有値\(\lambda_1\)と一致する.
次に,第\(k\)主成分得点\( k = (2,\ldots,p) \)は,標本分散共分散行列\(S\)の\(k\)番目に大きい固有値\(\lambda_k\)に対する固有ベクトル\(\boldsymbol \alpha_k\) を用いた次のような内積として定義される.
このとき,第1主成分と同様にこの標本分散は\( \lambda_k \)と一致する.
主成分分析の指標
次に,主成分分析の結果の指標として,それぞれ全分散\({\rm tr}(S)\)・寄与率\( {\rm cr}_i \)・累積寄与率\( {\rm ccr}_k \)を次のように定義する.
概要で説明したように,主成分分析では分散を情報と捉えている.寄与率は,各主成分が全体の情報のうち,どの程度 の情報量を持っているかを示す指標と考えることができる.もちろん,寄与率は各主成分の分散\( \lambda_i \)の値に 比例して大きくなるので,もっとも情報量が大きいのは第1主成分であり,それ以降第2主成分,第3主成分,という順番で 情報量は小さくなっていく.
また,累積寄与率が取りうる値は\( 0 \leq {\rm ccr}_k \leq 1 \)であり,1に近づくほどの元データが持つ情報量 を保持していると考えられる.もしたかだか\(k\)個\(k \leq p\)までの累積寄与率\( {\rm ccr}_k \)の値がほぼ1と なっていた場合,分散の意味での情報量は\(k\)個の変量で十分保持できており,データの次元削減にも用いることができる.
2次元データの例
視覚的に捉えやすいように2次元データを生成し,主成分分析による軸の回転を可視化しよう. いま\(x_{i1}, x_{i2}\)となる対のデータを40個生成し,相関係数は0.82程度である.このデータに対して 主成分分析を行なった結果の主成分得点のプロットが左図である.
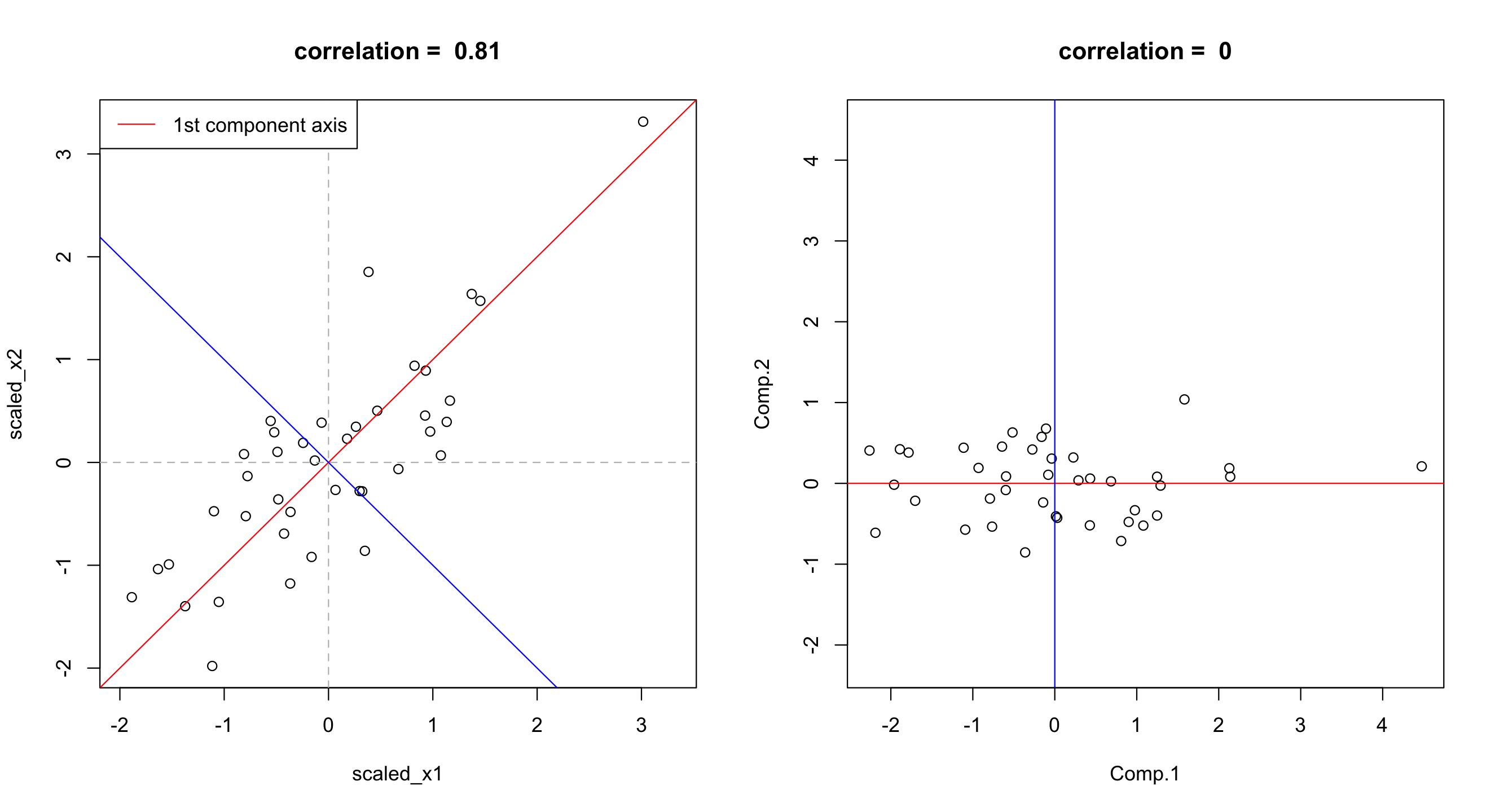
ここで,赤線は第1主成分軸,青線は第2主成分軸を表しており,主成分得点はこの第1主成分軸と第2主成分軸 が新たな座標軸となるように元のデータ点が回転したものと捉えられることがわかる.
アメダスのデータを用いた例
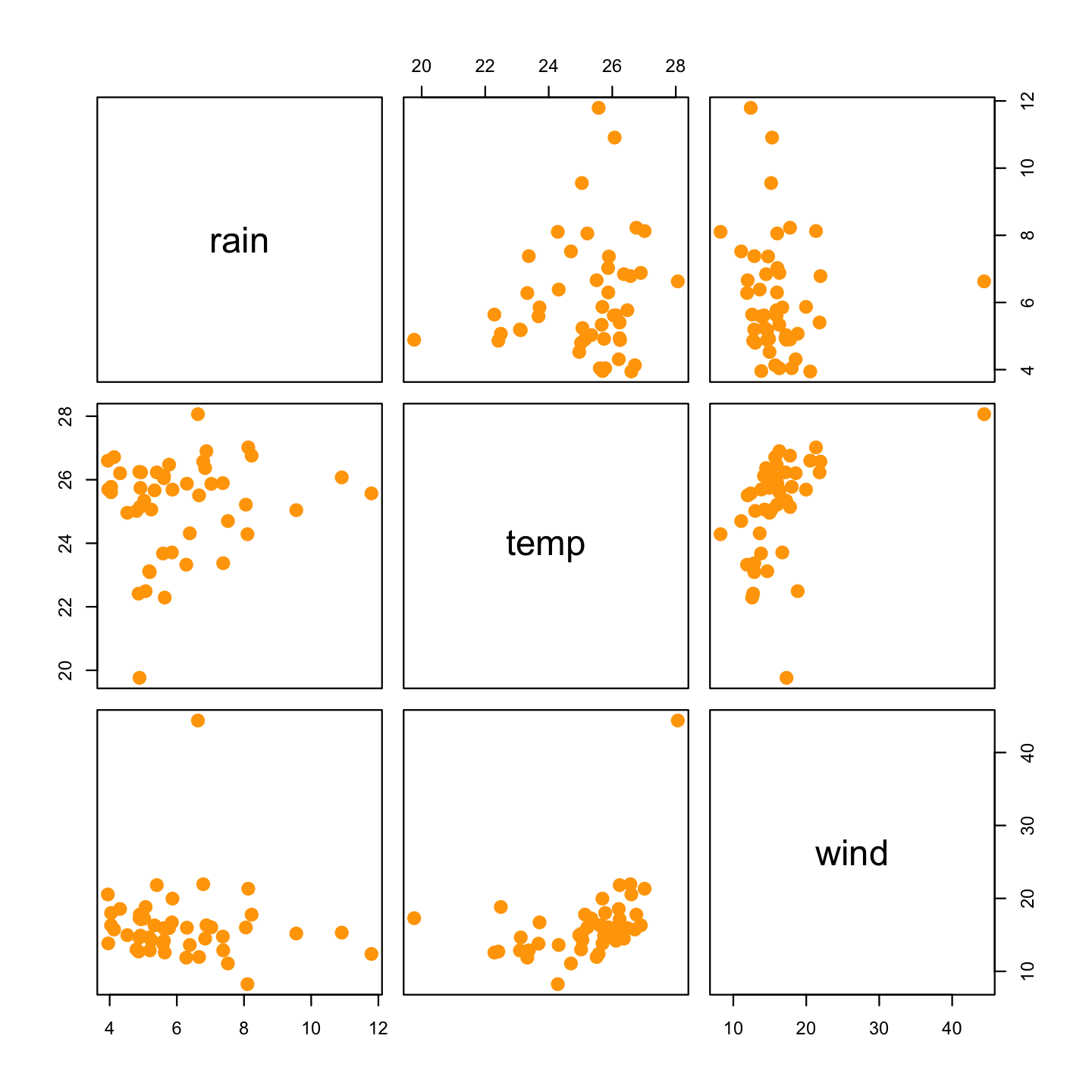
次に,アメダスの観測データを用いた主成分分析の応用例を紹介する.利用するデータは,アメダスの日毎の雨量・平均気温・平均風速の 観測データを各県ごとに平均し,さらに雨量の多い8月のみとした.データセットについてはページの最後に記載している. まず分布を確かめるために雨量・平均気温・平均風速のデータの散布図行列を見てみよう.相関係数は雨量と平均気温が0.14,雨量と平均風速が-0.08, 平均気温と平均風速が0.4という値になった.気温に関しては,飛び抜けて高い県と低い県があり,直感と同じくそれぞれ沖縄と北海道である.
| PC1 | PC2 | PC3 | |
|---|---|---|---|
| Standard deviation | 26.173 | 3.140 | 1.761 |
| Proportion of Variance | 0.842 | 0.101 | 0.057 |
| Cumulative Proportion | 0.842 | 0.943 | 1 |
次に,各主成分係数(固有ベクトル)を表2に示す.第1主成分だけでも80%の分散を保持できており, 平均風速に対応する値が大きいので第1主成分得点に関しては,平均風速の影響が高いことがわかる. 次に,第2主成分は雨量に対応する値が大きい.
| PC1 | PC2 | PC3 | |
|---|---|---|---|
| rain | 0.028 | -0.932 | 0.363 |
| temp | -0.138 | -0.363 | -0.922 |
| wind | -0.99 | 0.025 | 0.139 |
ここでもとの座標軸から第1,第2主成分ベクトルが張る平面への射影の様子を視覚化しよう. 次の3次元プロットは,マウスを合わせてドラッグすることで回転させることもできるのでためしてほしい. 青い平面が第1,第2主成分が張る平面であり,第1,第2主成分得点の値は,この平面に対して 直交する方向に各データ点を射影した時の座標と一致する.
最後に,第1,第2主成分得点による2次元のプロットを見てみよう.
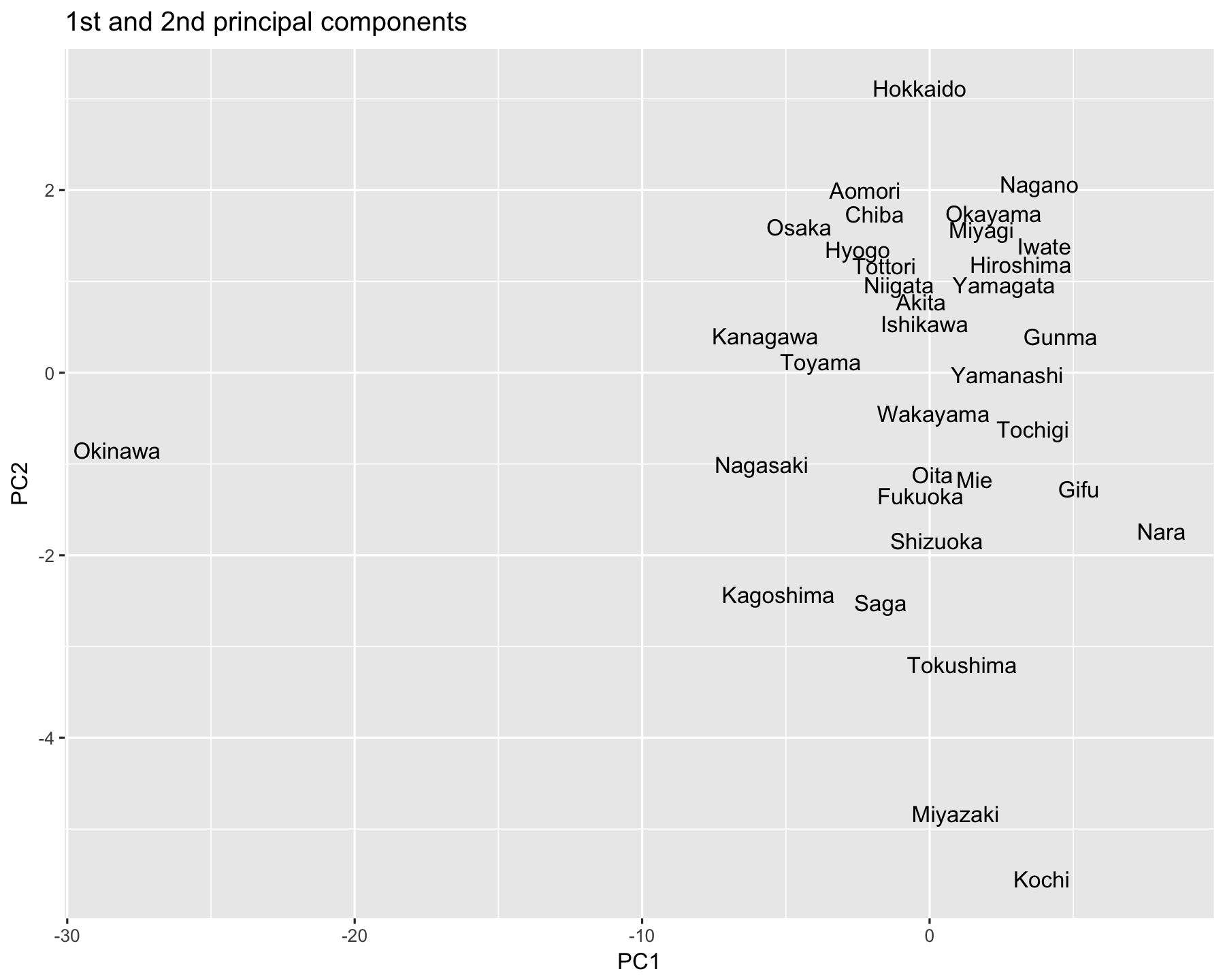
図4を見ると,沖縄は,第1主成分,第2主成分の軸から見ても他の県と大きく異なり,日本の中でも8月の気候が大きく ことなる地域であることがわかる.また,北海道は第1主成分の軸に関しては他の県と大きく変わらないが 第2主成分の軸に関しては大きい値を取っており,8月の雨量が飛び抜けて少なく,気温も低い地域という 特徴を捉えられている.一方,高知・宮崎も他の県から少し外れたところに位置しており, 雨が多く,気温が高い地域であることがわかる.
データセット
| rain | temp | wind | |
| Aomori | 5.069 | 22.492 | 18.827 |
| Akita | 5.852 | 23.71 | 16.718 |
| Iwate | 5.639 | 22.29 | 12.579 |
| Miyagi | 5.176 | 23.119 | 14.654 |
| Yamagata | 5.588 | 23.678 | 13.796 |
| Fukushima | 5.195 | 23.092 | 12.87 |
| Ibaraki | 4.525 | 24.96 | 14.968 |
| Tochigi | 7.38 | 23.372 | 12.881 |
| Gunma | 6.281 | 23.325 | 11.884 |
| Tokyo | 6.662 | 25.508 | 11.969 |
| Chiba | 4.043 | 25.777 | 18.007 |
| Kanagawa | 5.404 | 26.232 | 21.824 |
| Nagano | 4.862 | 22.414 | 12.716 |
| Yamanashi | 6.385 | 24.313 | 13.621 |
| Shizuoka | 8.055 | 25.215 | 16.016 |
| Aichi | 4.882 | 26.248 | 14.638 |
| Gifu | 7.52 | 24.699 | 11.081 |
| Mie | 6.842 | 26.367 | 14.491 |
| Niigata | 5.027 | 25.341 | 17.244 |
| Toyama | 5.869 | 25.689 | 19.97 |
| Ishikawa | 5.336 | 25.666 | 16.303 |
| Fukui | 4.934 | 26.232 | 17.15 |
| Shiga | 4.917 | 25.742 | 14.904 |
| Osaka | 3.945 | 26.6 | 20.544 |
| Hyogo | 4.309 | 26.205 | 18.553 |
| Wakayama | 6.299 | 25.876 | 15.991 |
| Okayama | 3.958 | 25.693 | 13.837 |
| Hiroshima | 4.799 | 25.018 | 13.001 |
| Shimane | 5.239 | 25.061 | 14.287 |
| Tottori | 4.899 | 25.142 | 17.786 |
| Tokushima | 9.556 | 25.042 | 15.189 |
| Kagawa | 4.131 | 26.713 | 15.736 |
| Ehime | 5.768 | 26.475 | 15.931 |
| Kochi | 11.795 | 25.571 | 12.388 |
| Yamaguchi | 5.613 | 26.048 | 15.927 |
| Fukuoka | 6.881 | 26.9 | 16.316 |
| Oita | 7.025 | 25.87 | 16.045 |
| Nagasaki | 6.785 | 26.571 | 21.946 |
| Saga | 8.226 | 26.758 | 17.777 |
| Kumamoto | 7.368 | 25.894 | 14.773 |
| Miyazaki | 10.91 | 26.074 | 15.31 |
| Kagoshima | 8.127 | 27.018 | 21.331 |
| Okinawa | 6.628 | 28.064 | 44.385 |
| Saitama | 5.616 | 26.12 | 14.198 |
| Kyoto | 4.041 | 25.607 | 16.315 |
| Hokkaido | 4.889 | 19.764 | 17.291 |
| Nara | 8.103 | 24.286 | 8.248 |