Let us start from the simple explanation of the least-squares method.
Let
$\{ ({a}_{i}, x_{i} )\}_{{i}=1}^{n}$ be a sequence in the two dimensional real space
${\mathbb R}^2$. Let
$\phi^{(\beta_1, \beta_2)}: {\mathbb R} \to {\mathbb R}$
be the simple function
such that
where
the pair
$(\beta_1, \beta_2) (\in {\mathbb R}^2 )$
is assumed to be unknown.
Define the error $\sigma_{}^{}$
by
This is easily solved as follows.
Taking partial derivatives with respect to
$\beta_0$,
$\beta_1 $,
and
equating the results to zero,
gives the equations
(i.e.,
"likelihood equations"),
Note that the above result is in (applied) mathematics,
that is,
Since quantum language says:
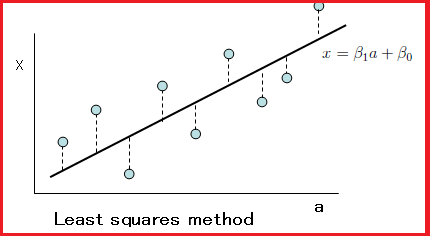 15.1 The least squares method
15.1 The least squares method
$\quad$
Let
$\{ ({a}_{i}, x_{i} )\}_{{i}=1}^{n}$ be a sequence in the two dimensional real space
${\mathbb R}^2$.
\\
Find the $(\hat{\beta}_0, \hat{\beta}_1)$
$( \in {\mathbb R}^2 )$ such that
\begin{align}
\sigma_{}^2
(\hat{\beta}_0, \hat{\beta}_1)
=
\min_{(\beta_1, \beta_2)
\in {\mathbb R}^2
}
\sigma_{}^2
(\beta_1, \beta_2)
\Big(
=
\min_{(\beta_1, \beta_2)
\in {\mathbb R}^2
}
\frac{1}{{n}}
\sum_{{i}=1}^{n}
(
x_{i} -( \beta_1 {a}_{i} + \beta_0 ))^2
\Big)
\tag{15.3}
\end{align}
where
$(\hat{\beta}_0, \hat{\beta}_1)$
is called
"sample regression coefficients".
Remark 15.2 [Applied mathematics]
$\bullet$
the above is neither in statistics nor
in quantum language.
the purpose of this chapter is to add a quantum linguistic story to Problem 15.1 (i.e., the least-squares method) in the framework of quantum language.
