Abstract (15.0: Least squares method and Regression analysis )
Abstract:
Although regression analysis has a great history, we consider that
it has always continued being confused.
For example,
the fundamental terms in regression analysis
(e.g.,
"regression", "least-squares method", "explanatory variable", "response variable", etc.)
seem to be historically conventional, that is, these words do not express the essence of regression analysis.
In this chapter,
we show that
the least squares method
acquires
a quantum linguistic story as follows.
\begin{align}
&
\underset{\mbox{(Section 15.1)}}{\fbox{The least squares method}}
\xrightarrow[\mbox{quantum language}]{\mbox{describe by}}
\underset{\mbox{(Section 15.2)}}{\fbox{Regression analysis}}
\nonumber
\\
&
\qquad \qquad \qquad
\xrightarrow[\mbox{generalization}]{\mbox{natural}}
\underset{\mbox{(Section 15.4)}}{\fbox{Generalized linear model}}
\tag{$\sharp$}
\end{align}
In this story,
the terms
"explanatory variable" and "response variable"
are clarified
in terms of quantum language.
As the general theory of regression analysis,
it suffices to devote ourselves to Theorem 13.4.
However, from the practical point of view,
we have to add the above story $(\sharp)$
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to
assert the following figure 1.1:
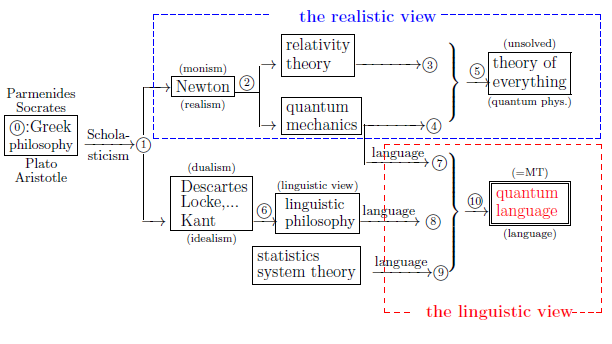
15.0 :Least-squares method and Regression analysis
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
