6.1 Review: classical quantum language(Axiom1)
Quantum language (= measurement theory ) is formulated as follows.
\begin{align}
&
\underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}}
:=
\underbrace{
\underset{\mbox{ ($\S$2.7)}}{
\overset{
[\mbox{ (pure) Axiom 1}]
}{\fbox{pure measurement}}
}
+
\underset{\mbox{ ($\S$10.3)}}{
\overset{
[{\mbox{ Axiom 2}}]
}{\fbox{Causality}}
}
}_{\mbox{ a kind of incantation (a priori judgment)}}
+
\underbrace{
\underset{\mbox{
($\S$3.1)
}}
{
\overset{
{}}{\fbox{Linguistic interpretation}}
}
}_{\mbox{ the manual on how to use spells}}
\tag{1.2}
\end{align}
where classical measurement is as follows.
Let ${\mathbb R}$ be the real axis. Define the state space $\Omega = {\mathbb R} \times {\mathbb R}_+$, where ${\mathbb R}_+=\{ \sigma \in {\mathbb R} | \sigma > 0 \}$ with the Lebesgue measure $\nu$. Consider the classical basic structure:
The normal observable ${\mathsf O}_{G} = ({\mathbb R}, {\mathcal B}_{\mathbb R}, {{{{G}}}} )$ in $L^\infty (\Omega (\equiv {\mathbb R} \times {\mathbb R}_+))$ is defined by
Let $n$ be a natural number. Let ${\mathsf O}_{G} = ({\mathbb R}, {\mathcal B}_{\mathbb R}, {{{{G}}}} )$ be the normal observable in $L^\infty ({\mathbb R} \times {\mathbb R}_+)$. Define the $n$-th simultaneous normal observable ${\mathsf O}_{G}^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{{G}}}^n} )$ in $L^\infty ({\mathbb R} \times {\mathbb R}_+)$ such that
Thus, we have the {simultaneous normal measurement} ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)} ({\mathsf O}_{G}^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{{G}}}^n} ), S_{[(\mu, \sigma )]})$.
Consider the maps $\overline{\mu}: {\mathbb R}^n \to {\mathbb R}$, ${\overline{SS}}: {\mathbb R}^n \to {\mathbb R}$ and ${\overline{\sigma}}: {\mathbb R}^n \to {\mathbb R}$ such that
 (A): Axiom 1(measurement) classical pure type
(A): Axiom 1(measurement) classical pure type
This can be read under the preparation ( $\S$2.7)
With any classical system $S$, a basic structure $[ C_0(\Omega) \subseteq L^\infty(\Omega, \nu )
\subseteq {B(L^2(\Omega, \nu ))}]$ can be associated in which measurement theory of that classical system can be formulated. In $[ C_0(\Omega) \subseteq L^\infty(\Omega, \nu ) \subseteq {B(L^2(\Omega, \nu ))}]$, consider a $W^*$-measurement ${\mathsf M}_{L^\infty(\Omega, \nu )} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[{}\delta_\omega] } \big)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{L^\infty (\Omega ) } \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[{}\delta_\omega] } \big)$ $\Big)$. That is, consider
Then, the probability that a measured value $x$ $( \in X )$ obtained by the $W^*$-measurement ${\mathsf M}_{L^\infty(\Omega, \nu )} \bigl({\mathsf O} , S_{[{}\delta_{\omega}{}] } \bigl)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{L^\infty (\Omega )} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[{}\delta_{\omega}] } \big)$ $\Big)$ belongs to $ \Xi $ $(\in {\cal F})$ is given by
\begin{align}
\delta_\omega( F(\Xi))
(\equiv [F(\Xi)](\omega)= {}_{{{\mathcal M}(\Omega)}}(\delta_{\omega}, F(\Xi) )_{L^\infty
(\Omega. \nu )} )
\end{align}
$\bullet$ a $W^*$-measurement ${\mathsf M}_{L^\infty(\Omega, \nu )} \bigl({\mathsf O} , S_{[{}\delta_{\omega}{}] } \bigl)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{L^\infty (\Omega)} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[{}\delta_{\omega}] } \big)$ $\Big)$ of an observable ${\mathsf O}{{=}} (X, {\cal F} , F)$ for a state $\delta_\omega (\in {\mathcal M}^p(\Omega):\mbox{;space})$
 In this chapter, we devote ourselves to the simultaneous normal measurement as follows.
In this chapter, we devote ourselves to the simultaneous normal measurement as follows.
Example 6.1 [Normal observable]
Example 6.2 [Simultaneous normal observable]
Therefore, we get and calculate (by the formulas of Gauss integrals ( in $\S$7.4) two image observables $\overline{\mu}({\mathsf O}_{G}^n) $ $= ({\mathbb R}, {\mathcal B}_{\mathbb R}, {{{{G}}}^n} \circ \overline{\mu}^{-1} )$ and ${{\overline{SS}}}({\mathsf O}_{G}^n) $ $= ({\mathbb R}_+, {\mathcal B}_{{\mathbb R}_+}, {{{{G}}}^n} \circ {{\overline{SS}}}^{-1} )$ in $L^\infty ({\mathbb R} \times {\mathbb R}_+)$ as follows.
\begin{align} & [({{{{G}}}^n} \circ \overline{\mu}^{-1})(\Xi_1)](\omega) \nonumber \\ = & \frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n} \underset{ \{ x \in {\mathbb R}^n \;:\; {\overline{\mu}}(x) \in \Xi_1 \}} {\int \cdots \int} \exp[{}- \frac{\sum_{k=1}^n ({}{x_k} - {}{\mu} )^2 } {2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n \nonumber \\ = & \frac{\sqrt{n}}{{\sqrt{2 \pi }\sigma{}}} \int_{{\Xi_1}} \exp[{}- \frac{n({}{x} - {}{\mu} )^2 }{2 \sigma^2} {}] d {}{x} \tag{6.6} \\ & \quad (\forall {\Xi_1} \in {\cal B}_{{\mathbb R}{}}, \;\; \quad \forall {}{\omega} =(\mu, \sigma) \in \Omega \equiv {\mathbb R}{}\times {\mathbb R}_+). \nonumber \end{align} and \begin{align} & [({{{{G}}}^n} \circ {{{\overline{SS}}}}^{-1})(\Xi_2)](\omega) \nonumber \\ = & \frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n} \underset{ \{ x \in {\mathbb R}^n \;:\; {\overline{SS}}(x) \in \Xi_2 \}} {\int \cdots \int} \exp[{}- \frac{\sum_{k=1}^n ({}{x_k} - {}{\mu} )^2 } {2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n \nonumber \\ = & \int_{\Xi_2 / \sigma^2} p^{{\chi}^2}_{n-1}({ x} ) {dx} \tag{6.7} \\ & \quad ( \;\; \forall \Xi_2 \in {\cal B}_{{\mathbb R}_+{}}, \quad \forall {}{\omega} =(\mu, \sigma) \in \Omega \equiv {\mathbb R}{}\times {\mathbb R}_+). \end{align}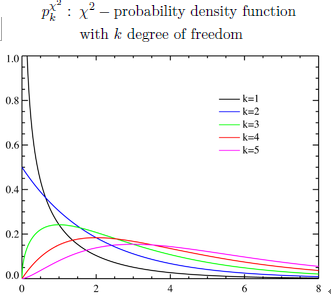
where $p^{{\chi}^2}_{n-1}({ x} )$ is the probability density function of $\chi^2$-distribution with $(n-1)$ degree of freedom. That is,
\begin{align} p^{{\chi}^2}_{n-1}({ x} ) = \frac{x^{(n-1)/2-1}e^{-x/2}}{2^{(n-1)/2} \Gamma ((n-1)/2)} \quad ( x > 0) \quad (6.8) \end{align} where,$\Gamma$ is the Gamma function.