[Abstract of Chap 3].
Measurement theory (= quantum language ) is formulated as follows.
\[
\underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}}
:=
\underbrace{
\underset{\mbox{ (\(\S\)2.7)}}{
\overset{
[\mbox{ (pure) Axiom 1}]
}{\fbox{pure measurement}}
}
+
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ Axiom 2}}]
}{\fbox{Causality}}
}
}_{\mbox{ a kind of incantation (a priori judgment)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{Linguistic interpretation}}
}
}_{\mbox{ the manual on how to use spells}}
\]
In the previous chapter (= Chap. 2 ), Axiom 1 was intruduced. In this chapter, I introduce "the linguistic interpretation", which is characterized as the manual on how to use axioms 1 and 2. Measurement theory says that
I believe that the Copenhagen interpretation is the ture color of the linguistic interpretation. And thus, it is also called "the linguistic Copenhagen interpretation".
$\bullet$
Describe every phenomenon modeled on Axioms 1 and 2(by a hint of the linguistic interpretation)!

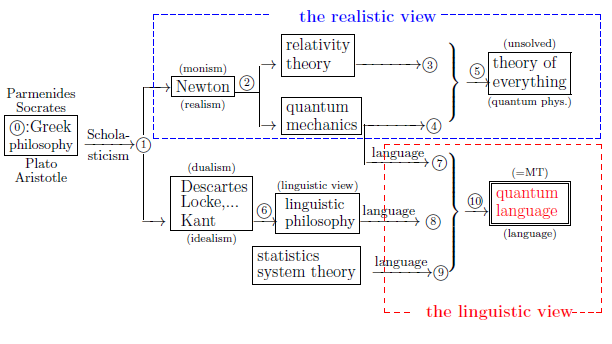
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to assert the following figure 1.1: