3.1.1 The review of Axiom 1 ( measurement: $\S$2.7)
In the previous chapter, we introduced Axiom 1 (measurement ) , which is mainly due to M. Born.
 3.1.1 The review of Axiom 1 ( measurement: $\S$2.7)
3.1.1 The review of Axiom 1 ( measurement: $\S$2.7)
With any system $S$, a basic structure $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$ can be associated in which measurement theory of that system can be formulated. In $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$, consider a $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$. That is, consider
| $\bullet$ | a $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[{}\rho{}] } \bigl)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$ of an observable ${\mathsf O}{{=}} (X, {\cal F} , F{})$ for a state $\rho(\in {\frak S}^p({\cal A}^*):\mbox{state space})$
|
Then, the probability that a measured value $x$ $( \in X )$ obtained by the $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[{}\rho{}] } \bigl)$ $\Big($ or, {$C^*$-measurement} ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$ belongs to $ \Xi $ $(\in {\cal F}{})$ is given by
\begin{align*}
\rho( F(\Xi))
(\equiv {}_{{{\mathcal A}^*}}(\rho, F(\Xi) )_{\overline{\mathcal A}} )
\end{align*}
(if $F(\Xi)$ is essentially continuous at $\rho$, or see (2.56) in Definition 2.19 ).
 Here, note that
Here, note that
| $(A):$ | the above axiom is a kind of spell (i.e., incantation, magic words, metaphysical statement), and thus, it is impossible to verify them experimentally.
|
In this sense, the above axiom corresponds to "a priori synthetic judgment" in Kant's philosophy.
And thus, we say:
| $(B):$ | After we learn the spell (= Axiom 1) by rote, we have to exercise and lesson the spell (= Axiom 1). Since quantum language is a language,
it may be unable to use well at first. It will make progress gradually, while applying a trial-and-error method.
|
However,
| $(C_1):$ | if we would like to make speed of acquisition of a quantum language as quick as possible, we may want the good manual on how to use the axioms.
|
Here, we think that
| $(C_2):$ |
the linguistic interpretation= the manual on how to use the spells (Axiom 1 and 2)
|
 After all, I want to assert that
\begin{align}
\underset{\mbox{[dualistic idealism]}}{\mbox{Descartes philosophy}}\longrightarrow
\left\{\begin{array}{ll}
\color{blue}{\underset{\mbox{[Axioms]}}{\mbox{Continental Rationalism}}}
\\
\\
\color{red}{\underset{\mbox{[Linguistic interpretation]}}{\mbox{British empiricism}}}
\end{array}\right\}
\longrightarrow \underset{\mbox{[quantum language]}}{\mbox{Kant philosophy}}
\end{align}
After all, I want to assert that
\begin{align}
\underset{\mbox{[dualistic idealism]}}{\mbox{Descartes philosophy}}\longrightarrow
\left\{\begin{array}{ll}
\color{blue}{\underset{\mbox{[Axioms]}}{\mbox{Continental Rationalism}}}
\\
\\
\color{red}{\underset{\mbox{[Linguistic interpretation]}}{\mbox{British empiricism}}}
\end{array}\right\}
\longrightarrow \underset{\mbox{[quantum language]}}{\mbox{Kant philosophy}}
\end{align}
3.1.2: Descartes figure (in the linguistic interpretation)
In what follows, let us explain the linguistic interpretation. The concept of "measurement" can be, for the first time, un erstood in dualism. Let us explain it. The image of "measurement" is as shown in Figure 3.1.
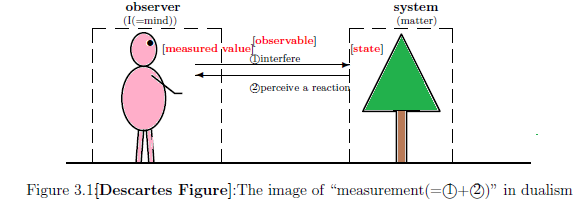 In the above,
In the above,
| $(D_1):$ | measurement = "① interfere" + "② perceive the reaction"
|
That is, "measurement" is characterized as the interaction between "observer" and "measuring object".
However, it can not be represented by a kinetic equation. (If the kinetic equation exists, we do not need dualism but monism.) Thus,
| $(D_2):$ | In measurement theory, we do not use the term "interaction" but "measurement".
|
Therefore, in order to avoid confusion, it might better to omit the interaction "① and ①" in Figure 3.1.
After all, we think that:
| $(D_3):$ | It is clear that there is no measured value without observer (i.e., brain).
Thus, we consider that measurement theory is composed of three key-words (cf. Note 3.1 later):
\begin{align}
\underset{\mbox{ (observer,brain, mind)}}{\fbox{measured value}}, \quad
\underset{\mbox{ (thermometer, eye, ear, body, polar star)}}{\fbox{observable (= measuring instrument )}},
\quad
\underset{\mbox{ (matter)}}{\fbox{state}},
\end{align}
and thus, it might be called "trialism" (and not "dualism"). But, according to the custom, it is called "dualism" in this note.
|
3.1.3: The linguistic interpretation $(E_1)-(E_7)$
The linguistic interpretation is "the manual on how to sue Axiom1 and 2". Thus, there are various explanations for the linguistic interpretations. However, it is usual to consider that the linguistic interpretation is characterized as the following (E). And the most important is
Only one measurement is permitted
(E):The linguistic interpretation (=quantum language interpretation)
With Descartes figure Figure 3.1 (and (E$_1$)-(E$_7$)) in mind, describe every phenomenon in terms of Axioms 1 and 2.
Here,
| $(E_1):$ | Consider the dualism composed of "observer" and "system( =measuring object)". And therefore, "observer" and "system" must be absolutely separated. If it says for a metaphor, we say "Audience should not be up to the stage".
|
| $(E_2)$: | Of course, "matter(=measuring object)" has the space-time. On the other hand, the observer does not have the space-time. Thus, the question: "When and where is a measured value obtained?" is out of measurement theory, Thus, there is no tense in measurement theory. This implies that there is no tense in science.
|
| $(E_3)$: | In measurement theory, "interaction" must not be emphasized.
|
| $(E_4)$: | Only one measurement is permitted. Thus, the state after measurement (or, the influence of measurement) is meaningless.
|
| $(E_5)$: | There is no probability without measurement.
|
| $(E_6)$: | State never moves,
|
and so on.
Also, since our assertion is
quantum language is the final goal of dualistic idealism
(="Descartes=Kant philosophy")
we have to assert that
| $(E_7)$: | Many of maxims of the philosophers (particularly, the dualistic idealism ) can be regarded as a part of the linguistic interpretation.
|
Some may think that the (E$_7$) is unbelievable. However, note that
| $(F_1):$ | the purpose of Descartes=Kant philosophy and that of quantum language are the same, that is, to establish the world view
|
| $(F_2)$: | the methodology of Descartes=Kant philosophy and that of quantum language are the same, that is, the non-realistic dualism.
|
Therefore, it is natual to consider
maxims of philosophers $\approx$ the linguistic interpretation
Recall the following figure ( in Chapter 1 ):
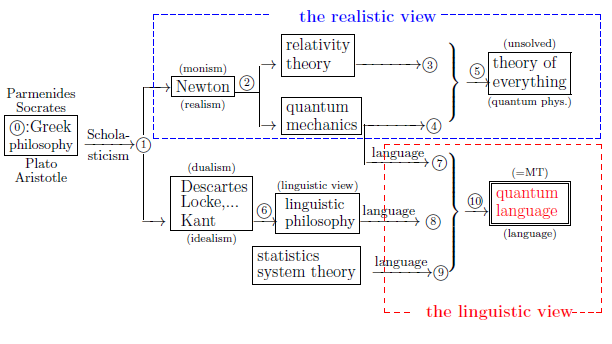 Fig.1.1: the location of "quantum language" in the world-views
In the above, we regard
Fig.1.1: the location of "quantum language" in the world-views
In the above, we regard
 as a genealogy of the dualistic idealism. Talking cynically, we say that
as a genealogy of the dualistic idealism. Talking cynically, we say that
| $\bullet$ | Philosophers continued investigating "linguistic interpretation" (="how to use Axioms 1 and 2") without Axioms 1 and 2.
|

For example, "Only one measurement is permitted" and "State never moves" may be related to Parmenides' words;
$
\left\{\begin{array}{ll}
\mbox{
There is no "plurality",
but only "one".
}
\\
\\
\mbox{
And therefore, there is no movement.}
\end{array}\right.
$
Thus, we want to assert that Parmenides (born around BC. 515) is the oldest discoverer of the linguistic interpretation.
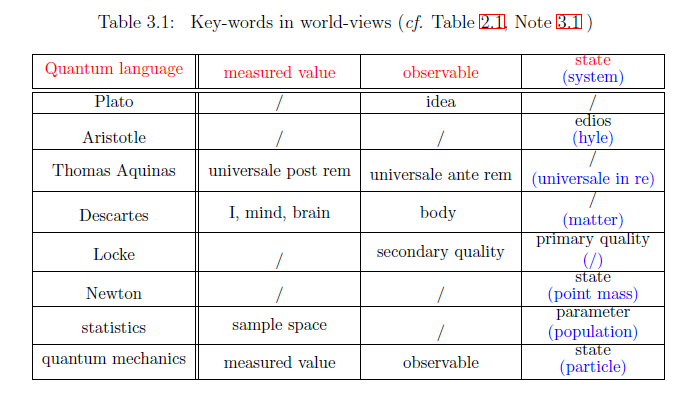
Also, we propose the following table:
 Although I am not familiar with ontology,
I want to consider "key-words exist in each world-view"
or
"Key-word = existence ".
Although I am not familiar with ontology,
I want to consider "key-words exist in each world-view"
or
"Key-word = existence ".
| $\fbox{Note 3.1}$ | In the above table, Newtonian mechanics may be the most understandable. Also, we want to identify "Plato idea" with "absolute standard". If the identification is permitted, we can understand that Table 3.1 implies Whitehead' word:
the development of Western philosophy is a series of footnotes to Plato
since each world-view including "observable" is regarded as dualistic idealism.
And, we want to understand that Newton is similar to Aristotle, since their assertions belong to the realistic world view (cf. Figure 1.1). Also, recall the formula (3.1), that is, "observable"="measuring instrument"="body". Thus, as the examples of "observable", we think:
$$
\mbox{
eyes,
ears,
glasses,
telescope,
compass,
etc.
}
$$
If "compass" is accepted, "the polar star" should be also accepted as the example of the observable. In the same sense, "the jet stream to an airplane" is a kind of observable. It is clear that there is no measured value without brain ( $\approx$ mind, brain ). Thus, we consider the correspondence :"measured value $\longleftrightarrow$ I". Also, if it is certain that Descartes is the first discoverer of "I", I have to retract our understanding of Scholasticism in Table 3.1. Although I have no confidence about Scholasticism, the discover of three words ("post rem", "ante rem", "in re") should be remarkable.
|
 3.1.1 The review of Axiom 1 ( measurement: $\S$2.7)
3.1.1 The review of Axiom 1 ( measurement: $\S$2.7)
 Here, note that
Here, note that






