3次方程式の解の公式
このページでは、多項式$$f(X) = X^3 + pX + q$$に対して $f(X)=0$の解を、$p,q$に四則演算と冪根を取るという操作を繰り返して得られる式で表すことを目指します。
$1$の$3$乗根と因数分解
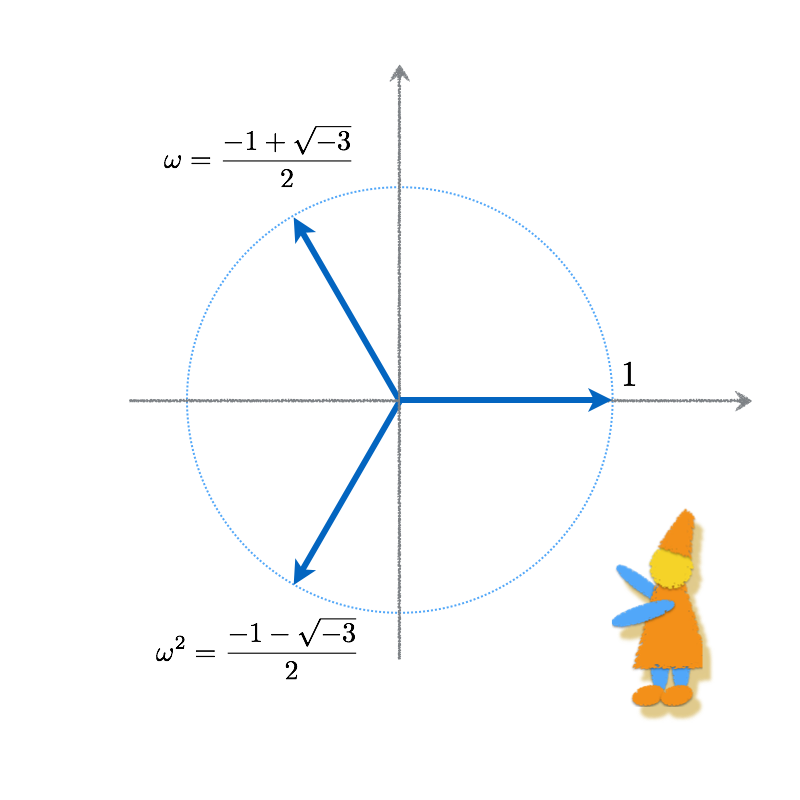
$\omega =\frac{-1 + \sqrt{-3}}{2}$と置くと、$\omega^2+\omega+1=0$が成り立ちます。従って、 \begin{multline} (X+Y+Z)(X+ \omega Y + \omega^2 Z)(X+ \omega^2 Y + \omega Z) \\ = (X+Y+Z) (X^2 + Y^2 + Z^2 + (\omega +\omega^2) XY + (\omega +\omega^2) XZ + (\omega +\omega^2) YZ) \\ = (X+Y+Z) (X^2 + Y^2 + Z^2 - XY - XZ-YZ) = X^3 + Y^3 + Z^3 - 3 XYZ \end{multline}
が成り立ちます。これは $X^3 + Y^3 + Z^3 - 3 XYZ$ が $$ X^3 + Y^3 + Z^3 - 3 XYZ = (X+Y+Z)(X+ \omega Y + \omega^2 Z)(X+ \omega^2 Y + \omega Z) $$ という形で因数分解することを意味しています。初めて見ると、とても難しい式に見えるかもしれませんが、 落ち着いてみると、両辺とも実際はとても対称性の高い式であることが分かります。 左辺を$X$について整理すると $$ X^3 - (3YZ) X + (Y^3 + Z^3) = (X+Y+Z)(X+ \omega Y + \omega^2 Z)(X+ \omega^2 Y + \omega Z) $$ となります。 この因数分解を利用して $$ f(X) = X^3 + pX + q = 0 $$ という形の方程式の解を求めることができます。上の式と比べると、 \begin{align} p &= -3YZ, & q&= Y^3 + Z^3 \end{align} とすれば、上の因数分解より$f(X)=0$の解は $$ X = -(Y+Z), \quad -( \omega Y + \omega^2 Z), \quad -( \omega^2 Y + \omega Z) $$ で与えられることが分かります。
因数分解の利用
従って、$f(X)=0$の解の公式を求める為には、$Y$と$Z$を$p$と$q$の式で書き下せば良い訳です。 $Y^3,Z^3$を$p, q$の式で表すと \begin{align} Y^3 + Z^3 &= q, & Y^3 Z^3 &= - \frac{p^3}{27} \end{align} となります。この2つの式と二次方程式の解と係数の関係から、$Y^3, Z^3$は $$ g(t) = (t - Y^3) (t - Z^3) = t^2 - (Y^3 + Z^3) t + Y^3 Z^3 = t^2 - q t - \frac{p^3}{27} = 0 $$ の解であることが分かります。従って、二次方程式の解の公式から $$ Y^3, Z^3 = \frac{q \pm \sqrt{q^2 + 4 p^3/27}}{2} $$ となります。従って、 $$ Y = \sqrt[3]{ \frac{q + \sqrt{q^2 + 4 p^3/27}}{2}} $$ と取ると、$YZ = -p/3$と $$ \biggl(\frac{q + \sqrt{q^2 + 4 p^3/27}}{2}\biggr)\biggl(\frac{q - \sqrt{q^2 + 4 p^3/27}}{2}\biggr) = \frac{q^2 - (q^2 + 4p^3/27)}{4} = - \frac{p^3}{27} $$ が成り立つことから、 $$ Z = \sqrt[3]{ \frac{q - \sqrt{q^2 + 4 p^3/27}}{2}} $$ となります。
$f(X)=X^3+pX+q=0$の解の公式
以上の考察から、$f(X) = X^3 + pX + q = 0$の解は \begin{align} & - \sqrt[3]{ \frac{q + \sqrt{q^2 + 4 p^3/27}}{2}}- \sqrt[3]{ \frac{q - \sqrt{q^2 + 4 p^3/27}}{2}} \\ & - \omega\sqrt[3]{ \frac{q + \sqrt{q^2 + 4 p^3/27}}{2}}- \omega^2\sqrt[3]{ \frac{q - \sqrt{q^2 + 4 p^3/27}}{2}} \\ & - \omega^2 \sqrt[3]{ \frac{q + \sqrt{q^2 + 4 p^3/27}}{2}}- \omega \sqrt[3]{ \frac{q - \sqrt{q^2 + 4 p^3/27}}{2}} \\ \end{align} の3通りであることが導かれます。
