CAT(k)空間

概要

内測平均(intrinsic mean)とは，ユークリッド空間における標本平均を，一般の測地距離空間へと自然に拡張したものであった．内測平均の一意性は，データが分布する空間の「曲率」に依存するが，それはリーマン幾何学的な曲率ではなくCAT(\(k\))性といわれる異なる種類の曲率により特徴づけされる．ここでは，\(k=0\)の場合であるCAT(\(0\))空間についての説明から始める．

CAT(\(0\))空間

まず，ここで測地距離空間とは，任意の二点間の距離がそれを結ぶ最短の曲線長と一致するような距離空間のこととする．測地距離空間\((\mathcal{X},d)\)上の任意の３点\(a,b,c\in \mathcal{X}\)に対し，ユークリッド平面上の３点\(a', b' ,c'\in\mathbb{R}^2\)が\(\|a'-b'\|=d(a,b)\)，\(\|b'-c'\|=d(b,c)\)，\(\|c'-a'\|=d(c,a)\)をみたすとき，三角形\(\Delta a'b'c'\)を測地三角形\(\Delta abc\)の（ユークリッド空間上の）比較三角形とよぶ．このとき，\(\mathcal{X}\)がCAT(0)空間であるとは，測地線上の任意の\(p\in \widetilde{bc}\)と，\(d(b,p) = \|b'-p'\|\)をみたす\(p'\in \overline{b'c'}\)に対して，\(d(a,p) \leq \|a'-p'\|\)が常に成り立つことである．

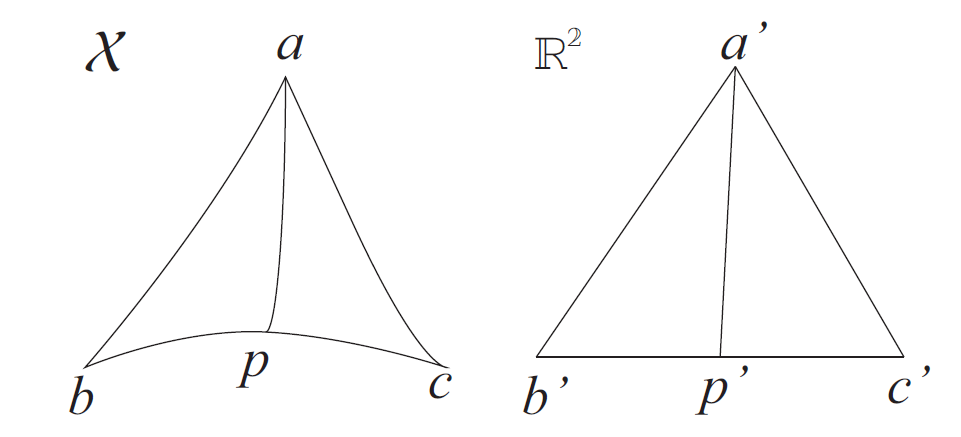
直感的には，\(\mathcal{X}\)上の測地三角形が，ユークリッド空間上の対応する比較三角形より「凹む」もしくは「痩せる」ような空間ということができる．また，\(\mathcal{X}\)がリーマン多様体の場合には，CAT(0)性を持つと，局所的には（断面曲率の意味で）非正曲率であることがいえる．

CAT(\(k\))空間と内測平均の一意性

より一般に\(k\in\mathbb{R}\)については，CAT(0)空間と同様にCAT(\(k\))空間が定義できる．ただし，３辺の長さの和が\(2\pi/\sqrt{\max(k,0)}\)以下であるような測地三角形の場合に限り，また，ユークリッド平面の代わりに，(リーマン断面曲率の意味で）曲率\(k\)の定曲率曲面上の測地三角形と比較する．この定義によると，リーマン多様体の場合にはCAT(\(k\))空間ならば局所的には（断面曲率の意味で）曲率が\(k\)以下であることがいえるこの事実からもわかるように，測地距離空間がCAT(\(k\))空間であるとき，\(k'\geq k\)に対してCAT(\(k'\))空間でもある．

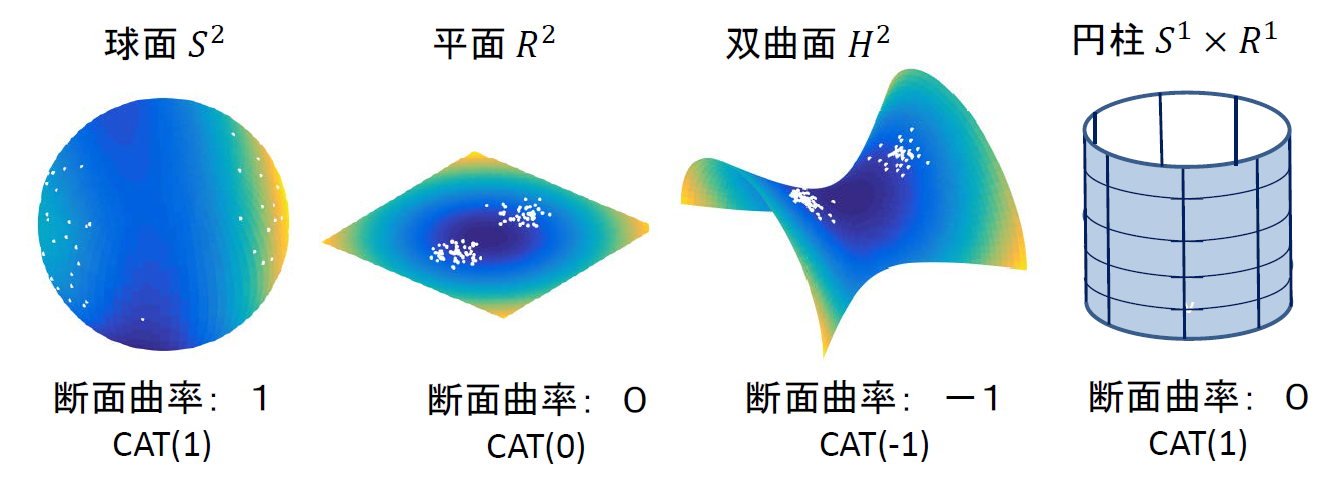
そして，CAT(0)空間上のデータに関しては，任意の２点間の測地線が一意に存在し，内測平均も常に一意に存在する．さらに一般に，CAT(\(k\))空間内の直径（もっとも離れた二点間の測地距離）が\(\pi/(2\sqrt{k})\)以下の領域上の確率分布は内測平均を持つことが証明できる．大雑把に言うと，CAT(\(k\))の意味での空間の曲率が小さいほど，その上のデータの内測平均はより一意になりやすいといえる．

図２においては，平面と双曲面はその上の任意のデータ点集合に対して内測平均が一意に存在するが，球面では一般には内測平均は一意になるとは限らないが，各点対の測地距離が\(\pi/2\)以下であれば，内測平均は一意に存在する．円柱面\(x^2+y^2=1,~z\in \mathbb{R}\)上の二点\((1,0,0)\)と\((-1,0,0)\)の内測平均は\((0,1,0)\)と\((0,-1,0)\)の二点となり，円柱面がユークリッド空間と同様にリーマン曲率0であるにもかかわらず，内測平均の一意性が成り立たない．