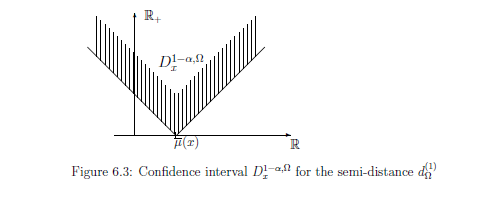
6.3(1): Population mean (Confidence interval )
Consider the classical basic structure:
\begin{align}
[ C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]
\end{align}
Fix a positive number $\alpha$ such that $0 < \alpha \ll 1$, for example, $\alpha = 0.05$.
6.3.1 Preparation (simultaneous normal measurement)
Example6.7 Consider the simultaneous normal measurement ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$ in $L^\infty({\mathbb R} \times {\mathbb R}_+)$. Here, the simultaneous normal observable ${\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n} )$ is defined by
\begin{align}
&
[{{{G}}}^n
({\mathop{\mbox{$\times$}}}_{k=1}^n \Xi_k)]
(\omega)
=
{\mathop{\mbox{ $\times$}}}_{k=1}^n
[{{{G}}}(\Xi_k)](\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{{{\mathop{\mbox{$\times$}}}_{k=1}^n \Xi_k }}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{x_k} - {}{\mu} )^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\tag{6.24}
\\
&
\qquad
(\forall \Xi_k \in {\cal B}_{{\mathbb R}{}}^{}
(k=1,2,\ldots, n),
\quad
\forall {}{\omega}=(\mu, \sigma ) \in \Omega = {\mathbb R}\times {\mathbb R}_+).
\nonumber
\end{align}
Therefore,the state space $\Omega$ and the measured value space $X$ are defined by
\begin{align}
&
\Omega = {\mathbb R} \times {\mathbb R}_+
\\
&
X={\mathbb R}^n
\end{align}
Also, the second state space $\Theta$ is defined by
\begin{align}
&
\Theta = {\mathbb R}
\end{align}
The estimator $E: {\mathbb R}^n \to \Theta (\equiv {\mathbb R} )$ and the system quantity$\pi: \Omega \to \Theta $ are respectively defined by
\begin{align}
&
E(x)=E(x_1, x_2, \ldots , x_n )
=
\overline{\mu}(x)
=
\frac{x_1 + x_2 + \cdots + x_n}{n}
\\
&
\Omega={\mathbb R} \times {\mathbb R}_+
\ni
\omega = (\mu, \sigma )
\mapsto \pi (\omega ) = \mu \in \Theta={\mathbb R}
\end{align}
Also, the semi-metric $d_{\Theta}^{(1)}$ in $\Theta$ is defined by
\begin{align}
d_{\Theta}^{(1)}(\theta_1, \theta_2)
=
|\theta_1 - \theta_2|
\qquad
(\forall \theta_1, \theta_2 \in \Theta ={\mathbb R})
\nonumber
\end{align}
6.3.2 Confidence interval
Our present problem is as follows.
Problem 6.8 [Confidence interval].
Consider the simultaneous normal measurement ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$. Assume that a measured value$x \in X ={\mathbb R}^n$ is obtained by the measurement. Let $0 < \alpha \ll 1$.
Then, find the ${D}_{x}^{1- \alpha; \Theta}( \subseteq \Theta)$ (which may depend on $\sigma$) such that
| $\bullet:$ | the probability that $\mu \in {D}_{x}^{1- \alpha; \Theta}$ is more than $1-\alpha$.
|
Here, the more ${D}_{x}^{1- \alpha; \Theta}( \subseteq \Theta)$ is small, the more it is desirable.
Consider the following semi-distance $d_{\Omega}^{(1)}$ in the state space ${\mathbb R} \times {\mathbb R}_+$:
\begin{align}
d_{\Omega}^{(1)}((\mu_1,\sigma_1), (\mu_2,\sigma_2))
=
|\mu_1 - \mu_2|
\tag{6.25}
\end{align}
For any $ \omega=(\mu, \sigma ) (\in\Omega= {\mathbb R} \times {\mathbb R}_+ )$, define the positive number $\delta^{1 - \alpha }_{\omega}$ $(> 0)$ such that:
\begin{align}
\delta^{1 - \alpha }_{\omega}
=
\inf
\{
\eta > 0:
[F (E^{-1} (
{{ Ball}_{d_\Omega^{(1)}}}(\omega ; \eta))](\omega )
\ge {1 - \alpha }
\}
\nonumber
\end{align}
where ${{ Ball}_{d_\Omega^{(1)}}}(\omega ; \eta)$ $=$ $\{ \omega_1 (\in\Omega): d_\Omega^{(1)} (\omega, \omega_1) \le \eta \}$ $= [\mu - \eta , \mu + \eta ] \times {\mathbb R}_+$
Hence we see that
\begin{align}
&
E^{-1}({{ Ball}_{d_\Omega^{(1)}}}(\omega ; \eta ))
=
E^{-1}([\mu - \eta , \mu + \eta ] \times {\mathbb R}_+)
\nonumber
\\
=
&
\{
(x_1, \ldots , x_n )
\in {\mathbb R}^n
\;:
\;
\mu - \eta
\le
\frac{x_1+\ldots + x_n }{n} \le \mu + \eta
\}
\tag{6.26}
\end{align}
Thus,
\begin{align}
&
[{{{G}}}^n
(E^{-1}({{ Ball}_{d_\Omega^{(1)}}}(\omega ; \eta ))]
(\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{{
\mu - \eta
\le
\frac{x_1+\ldots + x_n }{n} \le \mu + \eta
}}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{x_k} - {}{\mu} )^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{{
- \eta
\le
\frac{x_1+\ldots + x_n }{n} \le \eta
}}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{x_k} {}{} )^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
\end{align}
Using the Gauss integral (6.6), we see
\begin{align}
=
&
\frac{\sqrt{n}}{{\sqrt{2 \pi }\sigma{}}}
\int_{{- \eta}}^{\eta} \exp[{}- \frac{{n}{x}^2 }{2 \sigma^2}] d {x}
=
\frac{1}{{\sqrt{2 \pi }{}}}
\int_{{- \sqrt{n} \eta/\sigma}}^{\sqrt{n} \eta / \sigma} \exp[{}- \frac{{x}^2 }{2 }] d {x}
\tag{6.27}
\end{align}
Solving the following equation:
\begin{align}
\frac{1}{{\sqrt{2 \pi }{}}}
\int^{-z({ \alpha }/2)}_{-\infty} \exp[{}- \frac{{x}^2 }{2 }] d {x}
=
\frac{1}{{\sqrt{2 \pi }{}}}
\int_{z({ \alpha }/2)}^{\infty} \exp[{}- \frac{{x}^2 }{2 }] d {x}
=
\frac{\alpha}{2}
\tag{6.28}
\end{align}
we define that
\begin{align}
\delta^{1 - \alpha }_{\omega} =
\frac{\sigma}{\sqrt{n}}
z(\frac{\alpha}{2})
\tag{6.29}
\end{align}
Then, for any $x$ $(\in {\mathbb R}^n)$, we get $D_x^{{1 - \alpha }, \Omega}$ ( the $({1 - \alpha })$-confidence interval of $x$ ) as follows:
\begin{align}
D_x^{{1 - \alpha, \Omega }}
&
=
\{
{\omega}
(\in
\Omega)
:
d_\Omega (E(x),
\omega)
\le
\delta^{1 - \alpha }_{\omega }
\}
\nonumber
\\
&
=
\{ (\mu, \sigma ) \in {\mathbb R} \times {\mathbb R}_+
\;:\;
| \mu - \overline{\mu}(x)|
=
| \mu - \frac{x_1+ \ldots + x_n}{n}|
\le
\frac{\sigma}{\sqrt{n}}
z(\frac{\alpha}{2})
\}
\tag{6.30}
\end{align}
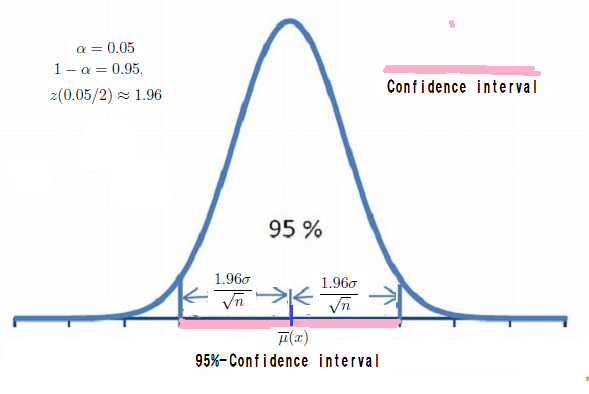 Also,
\begin{align}
D_x^{{1 - \alpha, \Theta }}
&
=
\{
\pi ({\omega})
(\in \Theta)
:
d_\Omega (E(x),
\omega)
\le
\delta^{1 - \alpha }_{\omega }
\}
\nonumber
\\
&
=
\{ \mu \in {\mathbb R}
\;:\;
| \mu - \overline{\mu}(x)|
=
| \mu - \frac{x_1+ \ldots + x_n}{n}|
\le
\frac{\sigma}{\sqrt{n}}
z(\frac{\alpha}{2})
\}
\nonumber
\end{align}
which depends on $\sigma$.
Also,
\begin{align}
D_x^{{1 - \alpha, \Theta }}
&
=
\{
\pi ({\omega})
(\in \Theta)
:
d_\Omega (E(x),
\omega)
\le
\delta^{1 - \alpha }_{\omega }
\}
\nonumber
\\
&
=
\{ \mu \in {\mathbb R}
\;:\;
| \mu - \overline{\mu}(x)|
=
| \mu - \frac{x_1+ \ldots + x_n}{n}|
\le
\frac{\sigma}{\sqrt{n}}
z(\frac{\alpha}{2})
\}
\nonumber
\end{align}
which depends on $\sigma$.