スプライン平滑化法

概要

統計的な枠組みにおける回帰や分類問題では，反応変量\(Y\)に対する共変量\(X\)を\(X\)の変換によって得られる新たな共変量を用いたりする場合がある．とくに，共変量\(X\)をある滑らかな関数の実現値と仮定し，その関数を推定することを平滑化と呼び，このときスプライン関数がよく用いられる．ここでは，スプライン平滑化の簡単な紹介と，スプライン平滑化のうち，自然３次スプライン（natural cubic spline），３次周期スプライン（cyclic cubic spline），そして薄板スプライン（thin plate spline）について紹介する．
スプライン平滑化は，周期性の可視化の際に，周期構造の推定のため用いている．

導入

まず，\( \{(x_i, y_i): \ i=1,\ldots,n \} \)というデータが与えられていて，この時\(x_i < x_{i+1}\)であるとする．ここで，\(y_i\)と\(x_i\)との間には，

\[ \begin{aligned} y_i = f(x_i) + \epsilon_i \end{aligned} \tag{1} \]

という関係があるとする．いま，与えられたデータからこの関数\(f(x)\)を推定したい．このようなときに用いられる手法が，スプライン平滑化法である．スプライン平滑化は基底関数法と呼ばれる手法の一つで，\(\beta_i\)を各基底関数\(b_i(x)\)の係数パラメータとして

\[ \begin{aligned} f(x) = \sum_{i=1}^{q} \beta_i b_i(x) \end{aligned} \]

という形で近似する．ここでどのように基底関数を定義するかという部分でスプライン法の中で種類が別れていく．

自然３次スプライン - natural cubic spline -

\(x_1 <\dots < x_k\)となるような点集合\((x_1,y_1),\dots,(x_k,y_k)\)が与えられたとき，その全てを通るような補間関数\(g(x)\)を考えよう．自然３次スプライン関数とは，このような補間関数のうち微分可能で，かつ各区間\([x_j,x_{j+1}]\)で３次関数であり，両端で二階微分がゼロ\(g ''(x_1)=g ''(x_k)=0\)となるような関数のことである．関数の滑らかさの基準として， \[ J(f):=\int_{x_1}^{x_n} f ''(x)^2 dx \] の小ささを用いるとしたとき（もっとも滑らかな場合は直線と考える），自然３次スプライン関数は（絶対連続な一階微分をもつ関数のうちで）最も滑らかな，つまり\(J(f)\)を最小にする補間関数である（Wood 2006の4.1.1節）．ただし，ここでいう「滑らかさ」は数学で通常用いられる定義とは異なるので注意が必要である．

次に，補間でなく(1)のような回帰分析の問題に対して，以下のような関数の最小化を考える．

\[ \begin{aligned} \sum_{i=1}^{n} \{ y_i - f(x_i) \}^2 + \lambda \int_{x_1}^{x_n} f''(x)^2 dx. \end{aligned} \]

ここで，第2項は「滑らかさ」を制御するための罰則項で，\(\lambda\geq 0\)は罰則の度合いを調節するパラメータである．特に，関数\(f\)を節点とよばれる\(k\)個の点\((\tilde{x}_1,f(\tilde{x}_1)),\dots,(\tilde{x}_k,f(\tilde{x}_k))\)（ただし\(\tilde{x}_1 <\dots <\tilde{x}_k\)）を補間する関数に限ったときには，自然３次スプライン関数が最小解となることがすぐにわかる．なおデータ解析においては，データ点集合の中から適当な方法で選んだものを節点とすることが多い．ただし，各節点での値\(f(\tilde{x}_i)\)はもちろんわからないから，これについては最適化で求める必要がある．

いま，\(\beta_j = f(\tilde{x}_j)\)，\( \delta_j = f''(\tilde{x}_j) \)とした時，自然スプライン関数は次のように表すことができる．

\[ \begin{aligned} f(x) = a^-_j(x)\beta_j + a^+_j(x)\beta_{j+1} + c^-_j(x)\delta_j + c^+_j(x)\delta_{j+1} \ {\rm if} \ \tilde{x}_j \leq x \leq \tilde{x}_{j+1} \end{aligned} \]

ここで，\(a^-_j, a^+_j, c^-_j, c^+_j\)は，\(h_j = \tilde{x}_{j+1} - \tilde{x}_j\)として次のように選ぶ．

表１　基底関数の定義



\(a^-_j(x)\)	\( = (\tilde{x}_{j+1}-x)/h_j \)
\(a^+_j(x)\)	\( = (x-\tilde{x}_{j})/h_j \)
\(c^-_j(x)\)	\( = [(\tilde{x}_{j+1}-x)^3/h_j - h_j(\tilde{x}_{j+1}-x)]/6 \)
\(c^+_j(x)\)	\( = [(x-\tilde{x}_{j})^3/h_j - h_j(x-\tilde{x}_{j})]/6 \)

また，自然３次スプラインでは各節点\(\tilde{x}_j\)における２次導関数は\(\delta_j\)，但し端点\(\tilde{x}_1=x_1, \tilde{x}_k=x_n\)における２次導関数の値を0とする．すなわち \(\delta_1 = \delta_k = 0\)とする．いま，\( \boldsymbol \delta^- = (\delta_2, \ldots, \delta_{k-1})^T \) として，表２のように定義される行列を用いて次が成り立つ．

\[ \begin{aligned} {\boldsymbol B} {\boldsymbol \delta}^- = \boldsymbol D \boldsymbol \beta \end{aligned} \tag{2} \]

表２　\( \boldsymbol B, \boldsymbol D \)　の非ゼロ要素
\( l=1,\ldots, k-1, \ m=1,\ldots,k-3 \)



\( D_{l,l} \)	\( = 1/h_l \)
\( D_{l,l+1} \)	\( = -1/h_l - 1/h_{l+1} \)
\( D_{l,l+2} \)	\( = 1/h_{l+1} \)
\( B_{m,m} \)	\( = (h_{m} + h_{m+1})/3 \)
\( B_{m,m+1} \)	\( = h_{m+1}/6 \)
\( B_{m+1,m} \)	\( = h_{m+1}/6 \)

この関係を利用すると先ほどのスプライン関数の表現は，\( \boldsymbol B^{-1} \boldsymbol D \boldsymbol \beta\)の \(j\)番目の要素を\( (\boldsymbol B^{-1}\boldsymbol D \boldsymbol \beta)_j \)として

\[ \begin{aligned} f(x) &= a^-_j(x)\beta_j + a^+_j(x)\beta_{j+1} + c^-_j(x)(\boldsymbol B^{-1}\boldsymbol D \boldsymbol \beta)_j + c^+_j(x)(\boldsymbol B^{-1}\boldsymbol D \boldsymbol \beta)_{j+1} ~~ \\ &\ {\rm if} \ \tilde{x}_j \leq x \leq \tilde{x}_{j+1} \end{aligned} \]

と表現でき，さらに右辺を\(\beta_i\)ごとにまとめて以下のように書き直す．\[ \begin{aligned} f(x) &= \sum_{i=1}^k \beta_i b_i(x) \end{aligned} \] ここで各\(b_i(x)\)は\(\tilde{x}_1,\dots,\tilde{x}_k\)の値のみにより定まり，これを自然３次スプラインの基底関数とみなすことができる．
式(2)より罰則項の部分は

\[ \begin{aligned} \int_{\tilde{x}_1}^{\tilde{x}_k} f''(x)^2 dx &= \boldsymbol \delta^{-T}\boldsymbol B \boldsymbol \delta^{-} = \boldsymbol \beta^{T} \boldsymbol D^{T} \boldsymbol B^{-1} \boldsymbol D \boldsymbol \beta \end{aligned} \tag{3}\]

と書き直せる．第一式は\[ \begin{aligned} \int_{\tilde{x}_{j}}^{\tilde{x}_{j+1}} f''(x)^2 dx &= \int_{\tilde{x}_{j}}^{\tilde{x}_{j+1}} \left\{\frac{\delta_j(\tilde{x}_{j+1}-x)}{h_j}+\frac{\delta_{j+1}(x-\tilde{x}_j)}{h_j}\right\}^2 dx \\ &= \delta_j^2\frac{h_j}{3} + \delta_{j+1}^2\frac{h_j}{3} + \delta_j\delta_{j+1}\frac{h_j}{6} \end{aligned} \] の両辺を\(j\)について和\(\sum_{j=1}^{k-1}\)をとれば確認できる．自然３次スプラインにおいては，式(3)を罰則項として最小化するような係数\(\boldsymbol \beta \)が選ばれる．ただし，\( \lambda \)の選択については一般化クロスバリデーション（GCV）などを用いて推定する必要がある．詳しくはWood(2006)を参照されたい．

3次周期スプライン - cyclic cubic spline -

3次周期スプラインは，始点と終点が滑らかに繋がるように基底関数を選ぶ方法である．これについては，自然３次スプラインにおける \( \boldsymbol B, \boldsymbol D \)を改めて\( \tilde{\boldsymbol B}, \tilde{\boldsymbol D} \)として，次のように選べば良い(Wood, 2006)．

表３　\( \tilde{\boldsymbol B}, \tilde{\boldsymbol D} \)　の非ゼロ要素
\( i=2,\ldots, k-1\)



\( \tilde B_{1,1} \)	\( = (h_{k-1}+h_1)/3 \)
\( \tilde D_{1,1} \)	\( = -1/h_1 - 1/h_{k-1} \)
\( \tilde B_{k-1,1} = \tilde B_{1,k-1} \)	\( = h_{k-1}/6 \)
\( \tilde D_{k-1,1} = \tilde D_{1,k-1} \)	\( = 1/h_{k-1} \)
\( \tilde B_{i-1,1} = \tilde B_{1,i-1} \)	\( = h_{k-1}/6 \)
\( \tilde D_{i-1,1} = \tilde D_{1,i-1} \)	\( = 1/h_{i-1} \)
\( \tilde B_{i,i} \)	\( = (h_{k-1}+h_1)/3 \)
\( \tilde D_{i,i} \)	\( = -1/h_1 - 1/h_{k-1} \)

以降は自然３次スプラインと同様，罰則項を行列\(\tilde{\boldsymbol B}, \tilde{\boldsymbol D}\)を用いて表現し直し，推定を行う．

人工データによるシミュレーション1

ここでは，次のような生成モデルからデータを500個発生させ，スプラインによる推定を行なってみる．まず生成モデルを次のように仮定する．

\[ \begin{aligned} y_i = \sin(x_i) + \epsilon_i \\ \epsilon_i \sim {\rm N}(0, 0.5^2) \end{aligned} \]

データ生成に関するRのコードを以下に示す．

                
                  ## A cyclic cubic spline
                  set.seed(200)
                  n <- 500
                  x <- seq(-2*pi, 2*pi, length.out=n)
                  y <- sin(x) + rnorm(n, 0, 0.5)

次に，生成データ，真の関数，周期スプライン法によって推定された関数と基底関数を合わせて図１に示す．推定の結果，基底関数の次元は10となっているが，定数項の部分は割愛している．一番上の図が，生成データに加えて赤の線が真の関数，緑の線が推定された関数を表している．基底関数の足しあわせによって，真の関数をほぼ近似できていることがわかる．Rのコードを以下に示す．

                  
                    fit_gam_cc <- gam(y~s(x, bs="cc"))

                    par(mfrow=c(3,3))
                    for(i in 1:9){
                      if(i==10){
                        plot(fit_gam_tp, xlab="", ylab="", main="Estimated and True function")
                        lines(x, sin(x), col="red")
                        legend("bottomleft", legend=c("Estimated", "True"), col=c("black", "red"), lty=1)
                      }else{
                        plot(model.matrix(fit_gam_tp) %*% diag(fit_gam_tp$coefficients)[,i], type="l",
                             xlab="", ylab="", main="basis function")
                      }
                    }

図１　周期スプライン法による推定結果

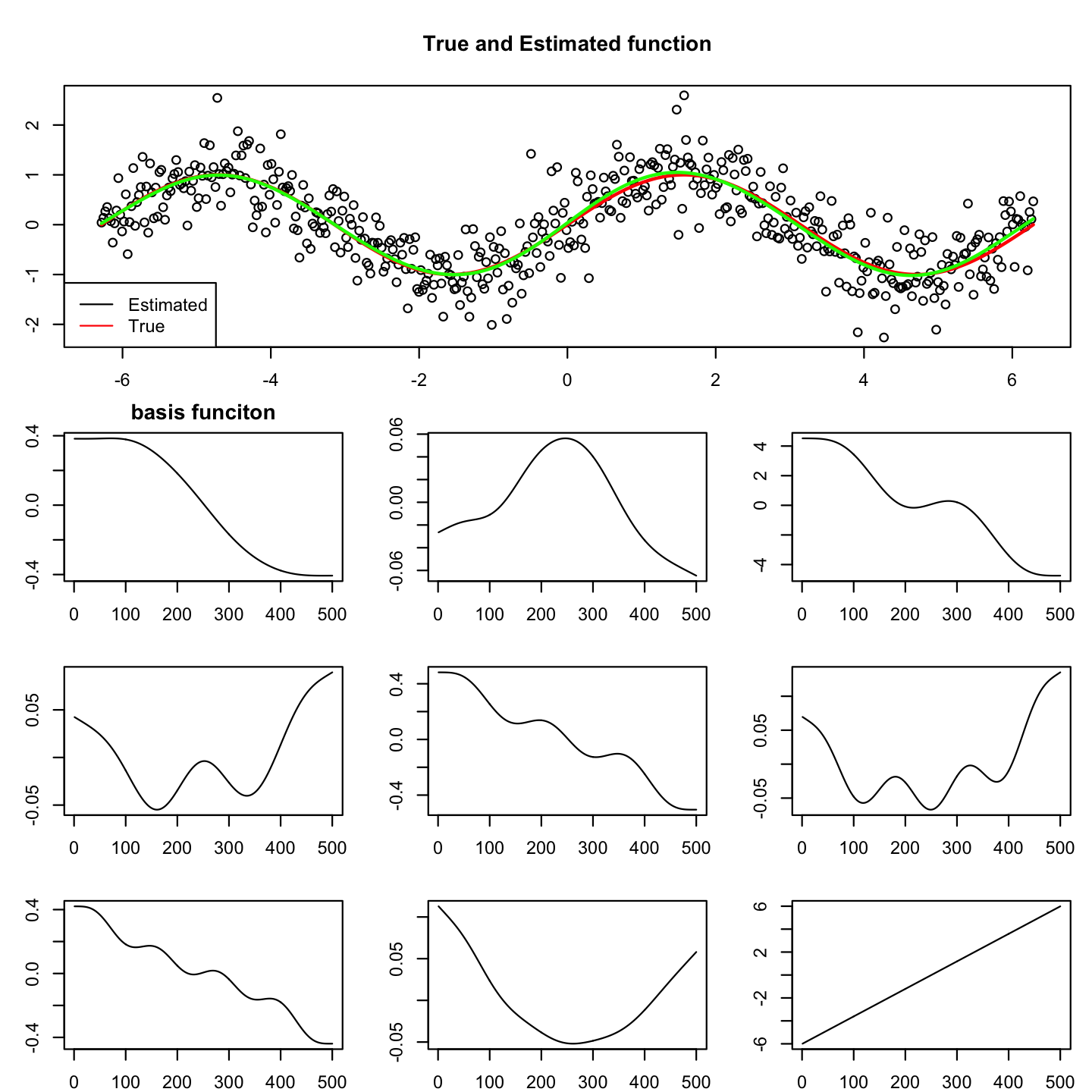
このように，データ解析において，データの背後になんらかの非線形な関数を仮定する場合，スプライン法による推定を用いるといくつかの基底関数を用いて目的の関数を近似できる場合がある．このような手法を一般的に基底関数法とも呼ぶ．

Thin plate spline法

これまでに紹介した自然３次スプライン法，周期スプライン法はいずれも単変量の場合のみを扱う．しかし，データの背後に多変量の関数を仮定する場合には使うことができない．そこで，多変量平滑法の一つであるThin plate spline法(Duchon, 1977)について紹介する．Thin plate spline法は，複数の共変量が誤差項を含む形で観測されている時，共変量を変数とする多変量平滑関数の推定に用いられる．まず，推定したい平滑化関数を\( g(\boldsymbol x) \)とし，\(　n \)対の観測値\( (y_i, \boldsymbol x_i) \)が与えられたとする．いま，次のような回帰モデルを考える．

\[ \begin{aligned} y_i = g(\boldsymbol x_i) + \epsilon_i \end{aligned} \]

ここで，\( \epsilon_i \)は観測誤差を表す確率変数，\( \boldsymbol x \)は\(d \leq n\)である\(d\)次元ベクトルである．Thin plate spline法では，\(g\)の推定を，次のような\(f\)に関する最小化問題に帰着させる．

\[ \begin{aligned} \| \boldsymbol y - \boldsymbol f \|^2 + \lambda J_{md}(f) \end{aligned} \]

ここで，\(\boldsymbol y\)は\(y_i\)を要素に持つ\(n\)次元ベクトル，\(\boldsymbol f\)は\(i\)番目の要素に\(f(x_i)\)を持つ関数値ベクトルである．また\(J_{md}(f)\)は関数\(f\)の滑らかさに対する罰則項であり，\(\lambda\)は平滑化パラメータである．\(J_{md}(f)\)は次のように定義される．

\[ \begin{aligned} J_{md}(f) = \int \cdots \int_{\mathcal{R}^d} \sum_{\nu_1 + \cdots + \nu_d = m} \frac{m!}{ \nu_1 ! \ldots \nu_d !} \left( \frac{\partial^m f}{ \partial x_1^{\nu_1} \cdots \partial x_d^{\nu_d} } \right)^2 dx_1 \ldots dx_d \end{aligned} \]

とくに簡単な場合である\(m = d = 2\)のときは以下のようになる．

\[ \begin{aligned} J_{22}(f) = \int \int_{\mathcal{R}^2} \sum_{\nu_1 + \nu_2 = 2} \frac{2!}{ \nu_1 ! \nu_2 !} \left( \frac{\partial^2 f}{ \partial x_1^{\nu_1} \partial x_2^{\nu_2} } \right)^2 dx_1 dx_2 \end{aligned} \]

これらの制約の下で，最適解は次のように表すことができる．

\[ \begin{aligned} \hat f(\boldsymbol x) = \sum_{i=1}^{n} \delta_i \eta_{md}(\|\boldsymbol x - \boldsymbol x_i \| ) + \sum_{j=1}^{M} \alpha _j \phi_j(\boldsymbol x) \end{aligned} \]

ここで，\(\boldsymbol \delta, \boldsymbol \alpha \)は推定された係数ベクトルであり，\(\boldsymbol\delta\)は\(T_{ij} = \phi_j(\boldsymbol x_i)\)に対して， \(\boldsymbol T \boldsymbol \delta = \boldsymbol 0\)を満たす．また，\(M = \frac{m+d-1}{d} \)である．上記に続き，特に簡単な\( (m=d=2) \)の場合は，\( \phi_1(\boldsymbol x) = 1, \phi_2(\boldsymbol x) = x_1, \phi_3(\boldsymbol x) = x_2 \)となる．一方，\(\eta_{md}\)については次のような形になることが知られている．

\[ \begin{aligned} \eta_{md}(r) = \begin{cases} \frac{(-1)^{m+1+d/2}}{2^{2m-1} \pi^{d/2} (m-1)! (m-d/2)!} r^{2m-d} \log(r) & d {\rm \ is \ even} \\ \frac{ \Gamma(d/2 - m) }{ 2^{2m} \pi^{d/2} (m-1)!} r^{2m - d} & d {\rm \ is \ odd} \end{cases} \end{aligned} \]

ここで，新たに\((i,j)\)成分が\( \eta_{md}(\| \boldsymbol x_i - \boldsymbol x_j\|) \)であるような行列\(\boldsymbol E\)を用いて最小化問題は次のように表せる．

\[ \begin{aligned} &\min_{\boldsymbol \delta, \boldsymbol \alpha}~~ \| \boldsymbol y - \boldsymbol E \boldsymbol \delta - \boldsymbol T \boldsymbol \alpha \|^2 + \lambda \boldsymbol \delta^{T} \boldsymbol E \boldsymbol \delta \\ &{\rm subject \ to \ }~~\boldsymbol T^{T} \boldsymbol \delta = \boldsymbol 0 \end{aligned} \]

人工データによるシミュレーション2

ここでは，次のような3次元データ\( (x_{i,1}, x_{i,2}, y_i) \)を900個発生させ，thin-plate-spline法により関数を推定する．

\[ \begin{aligned} y_i &= g(x_{i,1}, x_{i,2}) + \epsilon_i \\ g(x) &= \sin(0.5 x_1 + x_2) \\ 0.5 & \leq x_1, x_2 \leq 2.5 \\ \epsilon_i &\sim {\rm N}(0, \sigma^2) \end{aligned} \tag{3} \]

ただし，\( \epsilon_i \)は互いに独立とする．データ生成はRを用いて行った．コードは下記の通りである．

            
              f <- function(x, a=0.5){
                sin(a*x[1]+x[2])
              }

              x = seq(0.5, 2.5, by=0.05)
              X <- expand.grid(x,x)
              Y <- apply(X, 1, f)

              set.seed(100)
              s_num <- sample(size=30^2, x=1:nrow(X))
              dY <- Y[s_num] + rnorm(n=length(s_num), mean=0, sd=0.5)

              library(rgl)
              plot3d(x=X[s_num,1], y=X[s_num,2], z=dY, col="red", xlab="x1", ylab="x2", zlab="y")

生成データを3次元プロットで図２に示す．赤がデータ点である．

図２：(3)より生成したデータ

次に，thin plate spline法によって関数の推定を行う．ここでは，3次元プロットを用いて，生成関数と共変量によって推定された関数値を青い点で表示する（図３）．Rのコードは以下の通り

            
              fit_gam <- gam(dY~s(X[s_num,1], X[s_num,2], bs="tp"))
              plot(fit_gam$fitted.values, Y[s_num]); abline(a=0, b=1, col="red")

              library(rgl)
              plot3d(x=X[s_num,1], y=X[s_num,2], z=fit_gam$fitted.values, col="blue")
              surface3d(x=x, y=x, z=Y, col="lightgrey")

図３：真の関数（灰色）と推定点（青点）

灰色の面がデータ生成に用いた関数であり，青い点は共変量における関数値の推定結果である．概ね真の値に近いことがわかる．一方端点，特に\(x_1 = 0.5, x_2 = 0.5\)付近では推定精度があまり良くない．これは端点におけるサンプルサイズの影響と考えられる．

まとめ

このように，データから滑らかな関数を推定する際に，スプライン法は強力なツールとなり得る．どのように基底関数を選ぶかにより推定結果は変わるが，それは解析の際に仮定する関数との兼ね合いを考慮した上で選ぶのが良いだろう．多変量の場合，このほかにテンソルプロダクトを用いたスプライン平滑化法があるが，それは各変量に対して罰則パラメータを考えることができる（thin-plate-spline法では罰則パラメータは一つであった）．

参考文献

・Wood, S. N. (2006). Generalized additive models: an introduction with R. Chapman and Hall/CRC. ・Duchon, J. (1977). Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Constructive theory of functions of several variables (pp. 85-100). Springer, Berlin, Heidelberg.