降雨量データに基づく
日本地図の距離変換

概要

このデータ解析の目的は，標準的に用いられる緯度経度を用いた日本地図をアメダスによって観測された降雨量データに基づいた 尺度によって変形すること，またそれを考察することを目的とする．地域気象観測システム「アメダス」(Automated Meteorological Data Acquisition System)によって 日本全国約1,300箇所(約17km間隔)で日々降雨量データが記録されている．本解析では，一般財団法人 気象業務支援センターにて販売されているアメダスのデータを用いた． アメダスの観測所間の降雨量の相関係数と距離には明らかに非線形な関係があり，相関係数を距離の関数として表現できると考えられる． そこでまず，観測所間の降雨量の相関係数を距離によって回帰するモデルを推定する．次に，日本地図を覆うようにダミーの観測所点を追加した点を含め観測所点をドロネー分割を 用いて観測所間を辺で結ぶ．そして結ばれた観測所間の相関係数と距離を用いて観測所の点をある目的関数の最小化問題として移動させる． この時，ダミーの観測所との間の相関係数については推定したモデルによって補完する．最後に，観測所地点の移動結果を元に日本地図を変形させる．

解析に用いたデータ

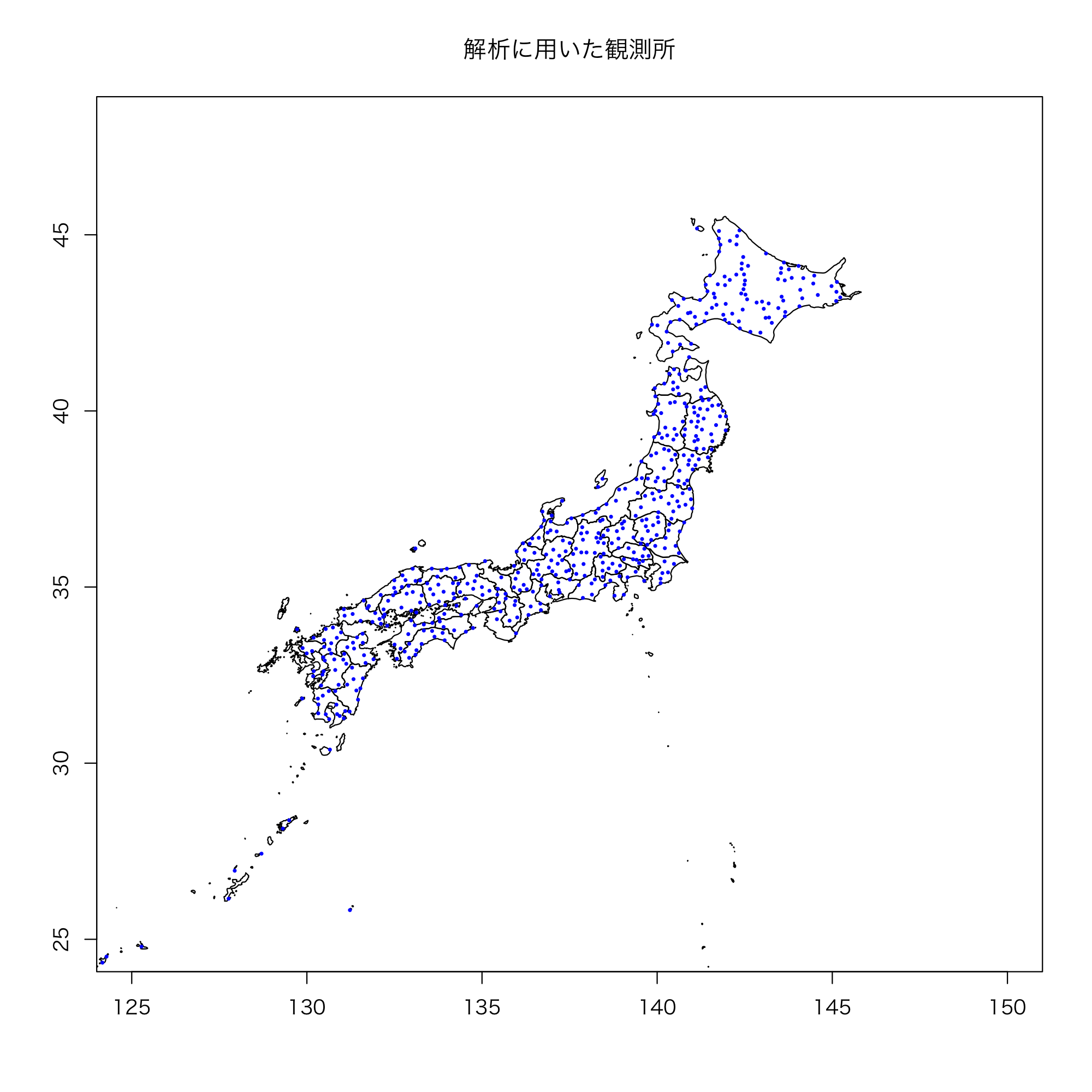
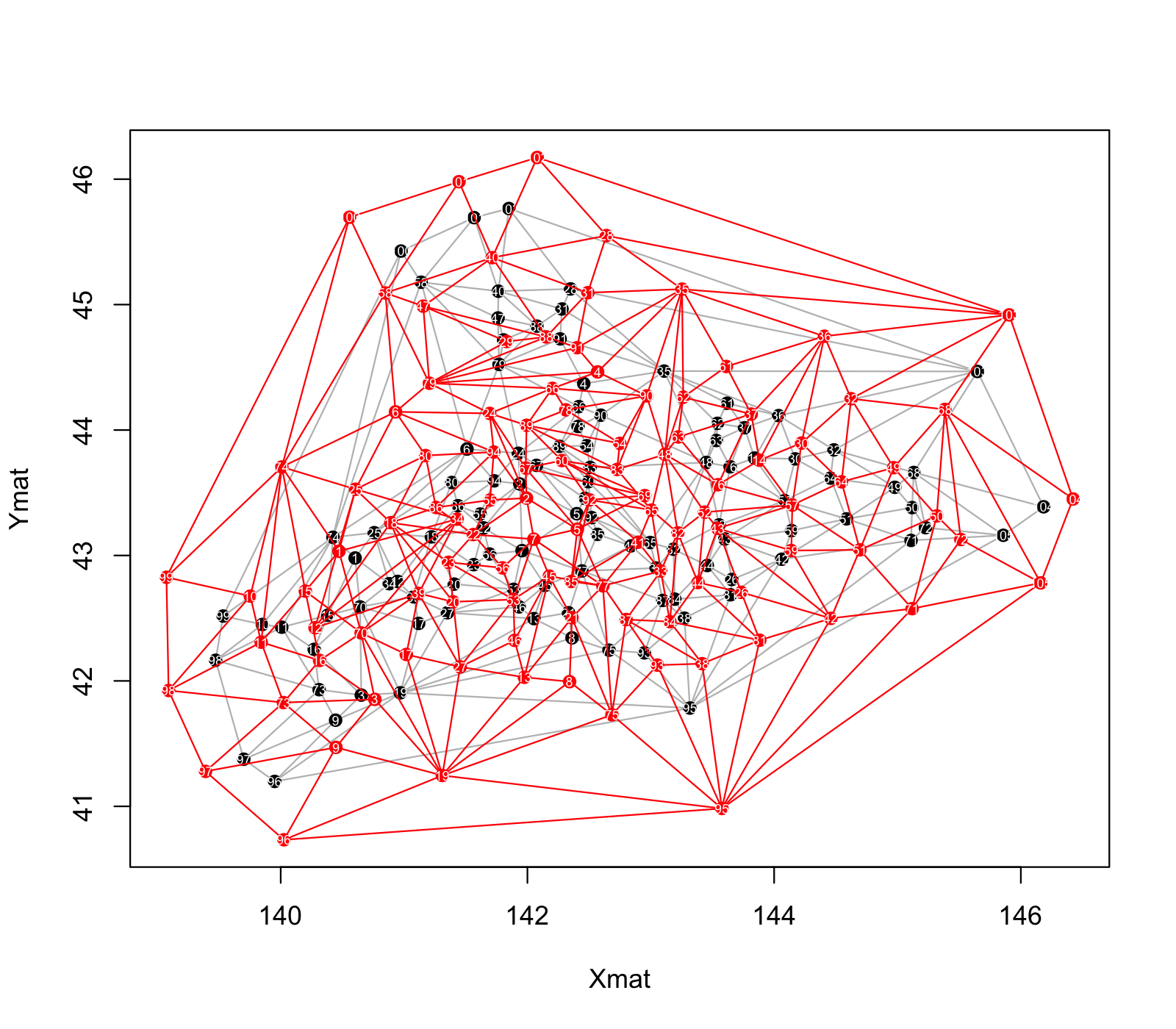
本解析には，一般財団法人 気象業務支援センターが発行するCDより，アメダスの降雨量データ及びWeb上にある日本の境界データ(http://www.naturalearthdata.com/downloads/10m-cultural-vectors/)を用いた． アメダスによるデータは1976年以降に記録されているが，欠測数が100以下になるよう期間と観測所を選び，実際には観測所は740箇所，期間は1980~2015年を用いた． 各観測所の位置については図１，各県ごとの観測所数は次の表１の通りである． 北方領土については観測点がないため，表示してない．

図１：解析に用いた観測所一覧


表１：都道府県ごとの観測所数
都道府県名 観測所数 都道府県名 観測所数 都道府県名 観測所数
北海道 94 山梨県 8 香川県 4
青森県 14 長野県 21 愛媛県 8
岩手県 28 岐阜県 18 高知県 11
宮城県 13 静岡県 10 福岡県 10
秋田県 18 愛知県 6 佐賀県 3
山形県 12 三重県 6 長崎県 2
福島県 19 滋賀県 6 熊本県 12
茨城県 10 京都府 2 大分県 9
栃木県 11 大阪府 6 宮崎県 9
群馬県 11 兵庫県 11 鹿児島県 17
埼玉県 6 奈良県 4 沖縄県 7
千葉県 6 和歌山県 3
東京都 4 鳥取県 6
神奈川県 3 島根県 11
新潟県 13 岡山県 13
富山県 6 広島県 12
石川県 8 山口県 12
福井県 6 徳島県 5

2 相関と距離の関係

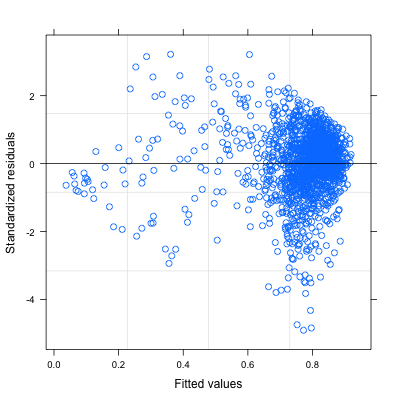
まず，各観測所間の距離と相関係数の散布図を図２に示す．距離が大きい観測所間ほど，相関が低くなっていることがわかる．


図２：距離と相関係数の散布図


図３：ドロネー分割の結果

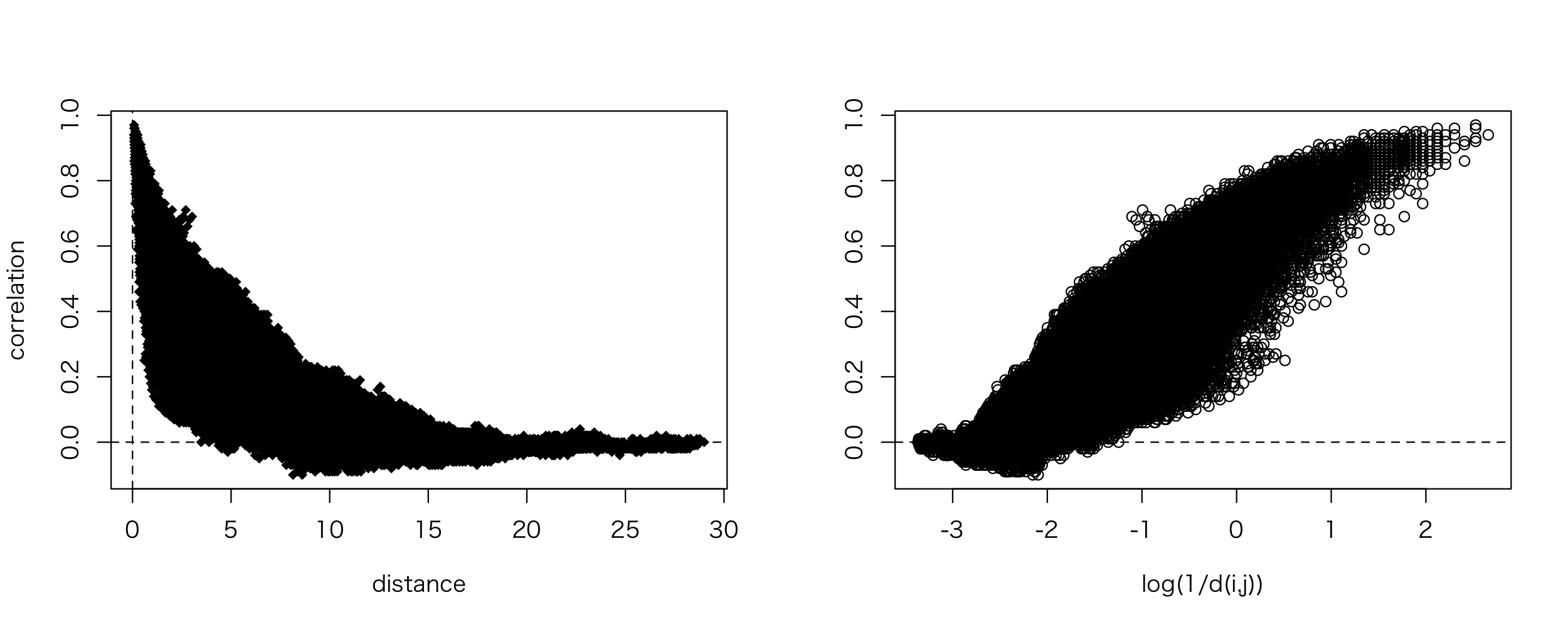
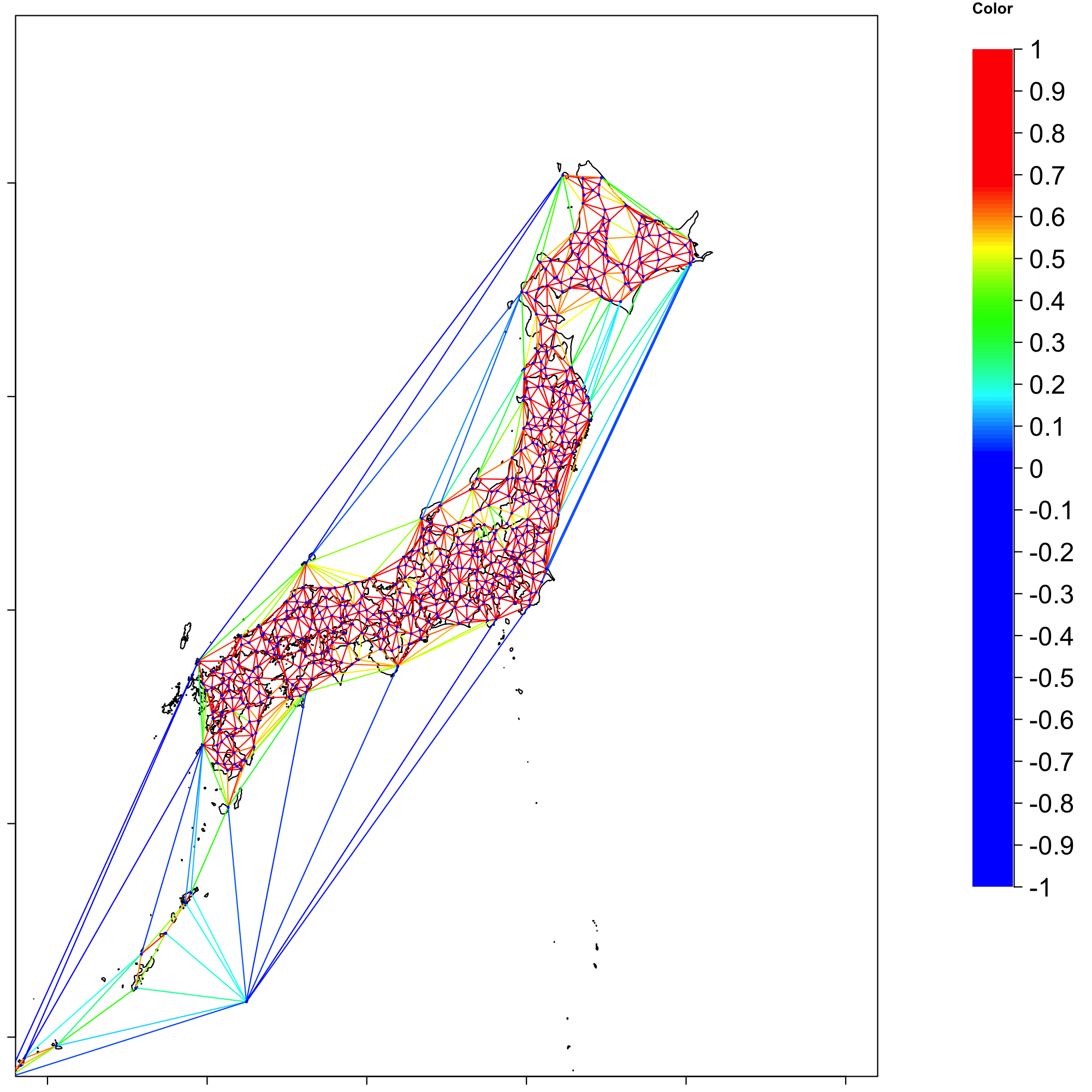
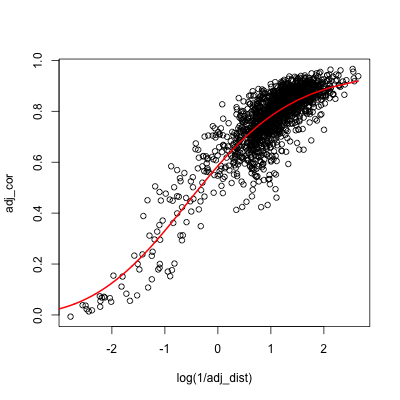
次に，各観測所の点をドロネー分割したグラフを考える．結果は図３のようになる．この時，辺の色は相関係数の値と対応させており，赤いほど値が1に近く， 青いほど値が0に近い．散布図で示したように，距離が小さい観測所間の相関は高く，距離が大きくなるほど低くなっていることがこちらの図でも見て取れる． 　ここで，距離によって相関係数の値を回帰することを考える．今はモデルの推定に用いる値はドロネー分割に対応するデータのみとした．距離の逆数の対数変換と相関係数の 散布図の傾向を考慮して，次のようなモデル（1）を仮定しパラメータを推定する．推定はRのnlm関数を用いた．推定結果を次の表２に示す．

回帰モデル \[ \begin{aligned} r(i,j) &= {a+b\exp(c \cdot d(i,j))} + \varepsilon_{(i,j)} \\ \varepsilon_{(i,j)} &\sim {\rm N}(0, \sigma^2) \end{aligned} \]

表２：回帰モデルの推定結果
Estimate Std.Error t value Pr(>|t|)
a \( 0.097 \) \( 0.016 \) -\(6.074\) \(1.56\times10^{-9}\)
b -\(0.833\) \(0.015\) -\(55.923\) \(2×10^{-16}\)
c \( -0.517 \) \( 0.021 \) \( -24.555 \) \( 2×10^{-16} \)

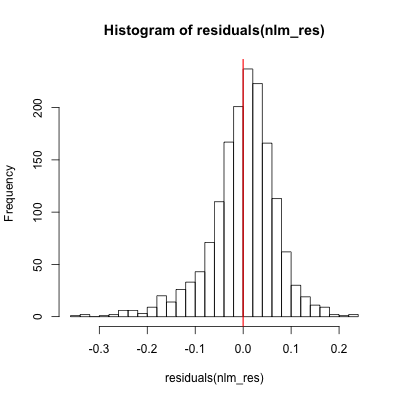
また，推定された曲線及び残差に関するプロットも図４に示す．

図４：回帰モデル１の推定結果

最小化問題による観測所地点の移動

次のような関数を目的関数(2)とした最小化問題を解くことで，降雨量の相関係数の尺度でドロネー分割の頂点を移動させる．

目的関数 \[ \begin{aligned} \min_{x_{1},\dots,x_{n}} \sum_{(i,j) \in \{(i,j)|A(i,j)=1\} } \| d(x_i,x_j) - \hat{d}_{ij}\|^2 + C \sum_{t=1}^{T} f(S_{\Delta_t}) \end{aligned} \tag{2} \]

ここで，\( \hat{d}_{ij} \)は相関係数から逆に計算された距離の推定値，\( A(i,j) \)はドロネー分割の辺による隣接行列，\( f(S_{\Delta_t}) \)はドロネー分割による各三角形の規格化逆面積，\(T\)はドロネー分割の三角形の数である．ここで，規格化逆面積は次のように計算される．

三角形の規格化逆面積 \[ \begin{aligned} f(S_{\Delta_t}) = \frac{|v_t^{(0)} \times w_t^{(0)}|}{|v_t^{(l)} \times w_t^{(l)}|} \end{aligned} \]

ただし，\( v_t^{(l)} \times w_t^{(l)} \)は \(l\) 回目の反復処理における外積による面積の計算である．

地図の変形

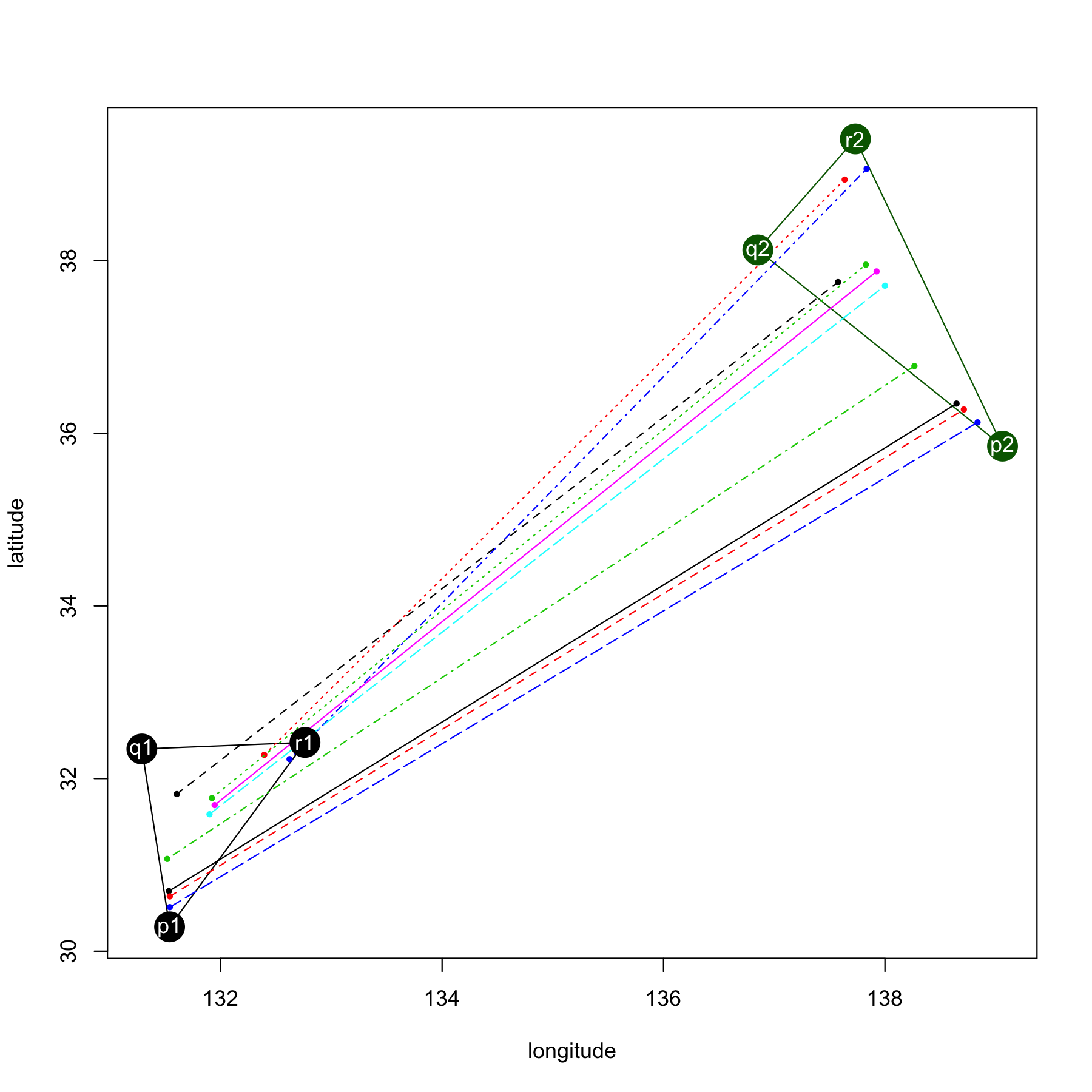
日本地図の境界線の変形については，アフィン変換によって行う．具体的には，境界線上の任意の点はドロネー分割によって生成された三角形のいずれかの内部に含まれる． さらに各三角形の頂点は上記の最適化によって移動する．そこで最適化前の三角形の内部の任意の点は最適化後の三角形の内部のある点と対応させることができる． 　いま，ある三角形の頂点をそれぞれ，\( {\boldsymbol p}_1, {\boldsymbol q}_1, {\boldsymbol r}_1 \)を考える． この時，三角形 \({\boldsymbol p_1}, {\boldsymbol q_1}, {\boldsymbol r_1} \)の任意の内部の点\( \boldsymbol x \)は次のように表せる．

\[ \begin{aligned} & {\boldsymbol x} = s (\boldsymbol p_2 - \boldsymbol p_1) + t (\boldsymbol p_3 - \boldsymbol p_1) + \boldsymbol p_1 \\ & s + t \leq 1 \\ & s,t \geq 0 \end{aligned} \]

つまり，異なるもう一つの三角形を考え，その頂点を\( {\boldsymbol p}_2, {\boldsymbol q}_2, {\boldsymbol r}_2 \) とした時，\(s,t\)によって任意の2つ三角形の内部の点を1対1に対応させることができる．三角形の頂点の座標を定め，内部の点を一つ選んだ時，\(s,t\)は一意に定まるので， これを用いて日本地図の境界線を変形させる．以下に，異なる2つの三角形の内部の点を対応させたサンプルを図５に示す．

図５：アフィン変換による任意の三角形間の点の対応付け

結果と考察

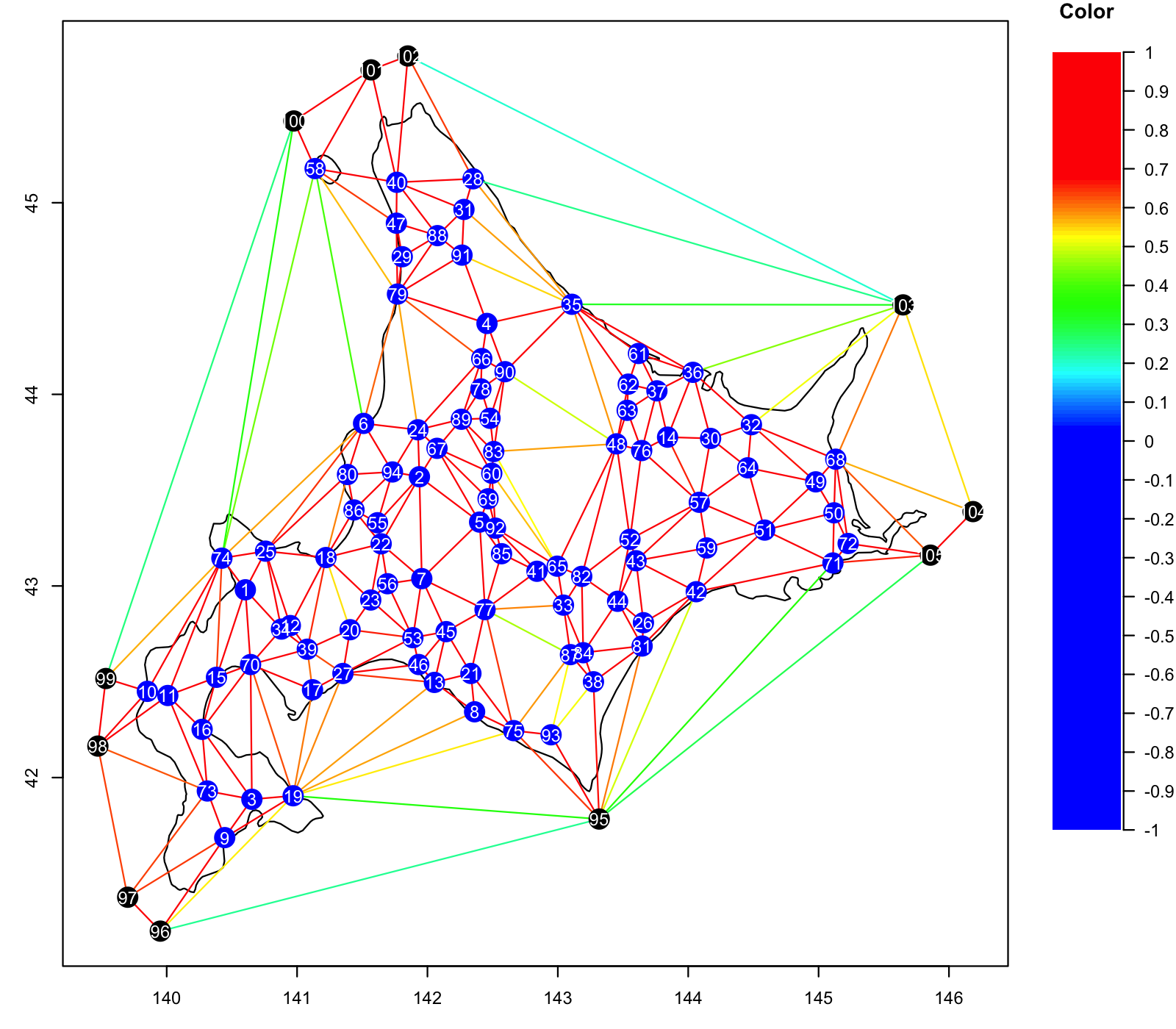
以下の３つの図６，図７，図８が北海道地方における変形の結果である．図６の図が観測所地点（ダミーの点を含む）とそのドロネー分割であり，辺の色は相関係数の値に応じて 右にあるカラーバーと対応するように付けている．図７の図は，各地点の最適化前後の比較の図である．図８の図が最適化した点を用いて地図を変形した図である． 北海道においては，下の部分がやや膨らんでいることから，平均的な相関と距離の関係よりも距離に比べて相関が低く，一方北東部はやや縮んでいるので， 平均的な距離と相関の関係よりも相関が高い傾向にあることがわかる．このように，本手法を用いることで地域の関係を表す指標によって，地域間の 距離を変えた地図を描く可能となる．

図６：観測所とドロネー分割，黒い点はダミーの点
図７：最適化の前後の頂点の比較，赤：最適化した頂点，青：元々の頂点
図８：頂点の移動による地図変形の結果，赤：変形後，灰色：変形前

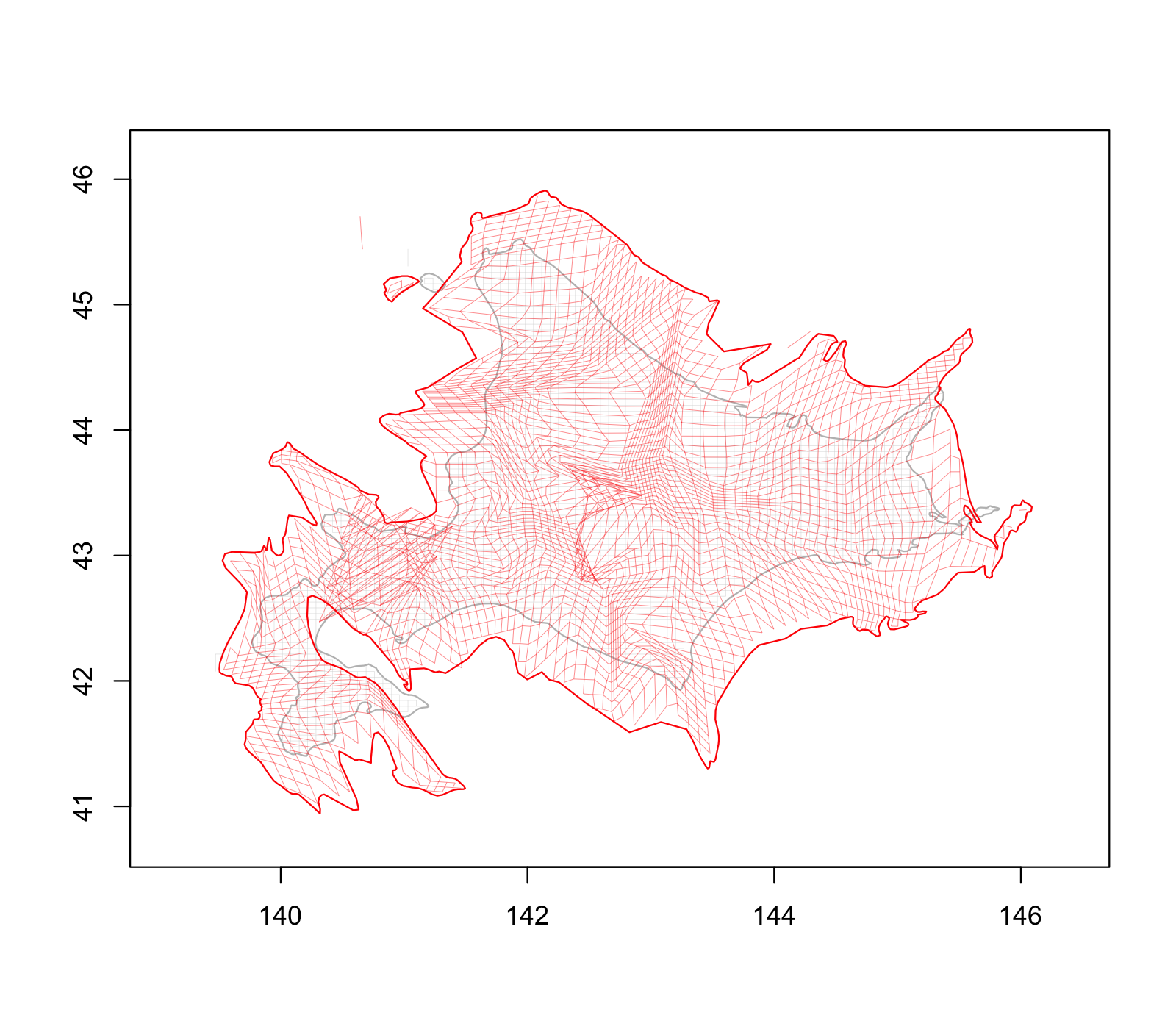
その他の地方区分における変形の結果についてはこちらのページを参照されたい．