行列の固有値と固有ベクトル
概要
ここでは,行列の固有値と固有ベクトルについて簡単に紹介する.統計学において,特に主成分分析において固有値・固有ベクトルは 重要な役割を果たしている.その他にも固有値・固有ベクトルによる行列の分解などが応用されることも多い. 本webサイトの解析レポートにおける周期性の可視化や,降雨量の一般化分散では,解析の過程で主成分分析を用いているため, 行列の固有値・固有ベクトルといった概念もこれらに関連している.
定義
いま,\(m\)次正方行列を\(A\)とする.この時,ある\(m\)次ベクトル\(\boldsymbol x \neq \boldsymbol 0\)とスカラー\(\lambda\)が存在して,次式が成り立つ時, \(\lambda\)を\(A\)の固有値,\(\boldsymbol x\)を\(A\)の固有値\(\lambda\)に対応する固有ベクトルという.
行列\(A\)とベクトル\(\boldsymbol x\)の積が,ベクトル\(\boldsymbol x\)の定数倍になっている, すなわち行列\(A\)という変換の結果,ベクトル\(\boldsymbol x\)の向きが(逆向きも含めて)変わらないという関係である. ここで,\(m\)次の単位行列\(I_m\)を用いて式(1)を次のように表し直すことができる.
式(2)において,もし逆行列\( (A- \lambda I_m)^{-1} \)が存在するとすると,\(\boldsymbol x \neq 0 \)という仮定に矛盾するため, \( |A- \lambda I_m| = 0 \)が導かれる.これは,\( \lambda \)に関する\( m \)次の多項式と同義であり, この\(m\)次多項式の\(m\)個の根に対応して固有ベクトルも\(m\)個存在することがわかる.特に主成分分析では, \(m\)個の固有値を大きい順に\(\lambda_1, \ldots, \lambda_m\)と表記することが多い.
基本的な性質
行列の固有値・固有ベクトルにおける基本的な性質は以下に述べる.ここで,\(A\)を\(m\)次行列, \(\lambda_i\)(\(i=1,\ldots,m\))を\(A\)の固有値とする.
- \(m\)次行列の固有値は重解も含めて\(m\)個存在する.
- \(\sum_{i=1}^{m} \lambda_i = {\rm tr}(A)\)が成り立つ.
- \(A^{T}\)の固有値は\(A\)の固有値と等しい.
- 対称行列の固有値は全て実数であり,固有ベクトルは互いに直行する.
- \(|A| = 0 \) ならば,固有値のうち少なくとも1つは0となるものがある.
- \(A\)が三角行列であるならば,\(A\)の対角要素が\(A\)の固有値と等しい.
Rにおける計算
Rにおける行列の固有値・固有ベクトルの計算方法を紹介する.Rではデフォルトで固有値・固有ベクトルを計算するeigen()関数が 用意されており,引数に行列を指定するだけで計算を実行してくれる.
#==============
# Rで固有値と固有ベクトルを求める
#==============
## 乱数固定
set.seed(100)
## 1~40までの要素を持つ行列を作成
A <- matrix(sample(size=16, x=1:40, replace=TRUE), nrow=4, ncol=4)
# [,1] [,2] [,3] [,4]
# [1,] 13 19 22 12
# [2,] 11 20 7 16
# [3,] 23 33 25 31
# [4,] 3 15 36 27
## 固有値・固有ベクトルを求める
eigen_A <- eigen(A)
## 固有値の出力
eigen_A$values
# [1] 79.998009 -9.600489 7.817493 6.784987
## 固有ベクトル(列ベクトル)の出力
eigen_A$vectors
# [,1] [,2] [,3] [,4]
# [1,] 0.4020977 0.4875738 0.7881439 0.7975726
# [2,] 0.2995325 -0.3917778 -0.2549961 -0.3688309
# [3,] 0.6619352 -0.4925824 0.2944885 0.2970304
# [4,] 0.5571709 0.6050988 -0.4765319 -0.3736504
最後に,Rを用いて固有ベクトルが行列\(A\)により定数倍される様子を可視化してみよう.
#==============
# 行列と固有値と固有ベクトルの関係を可視化
#==============
## 2次正方行列を生成
set.seed(100)
A <- matrix(sample(size=4, x=1:10, replace=TRUE), nrow=2, ncol=2)
eigen_A <- eigen(A)
## 固有ベクトルを一つ選ぶ
x <- eigen_A$vectors[,1]
Ax <- A %*% x ## 行列Aとの内積
## 固有ベクトルでないベクトルを一つ選ぶ
a <- c(1, 2)
Aa <- A %*% a
## matplot用の行列を作成
matX <- rbind(0, c(x[1], Ax[1], a[1], Aa[1]))
matY <- rbind(0, c(x[2], Ax[2], a[2], Aa[2]))
matplot(matX, matY, type="l", lwd=2, lty=1)
arrows(x0=0, y0=0, x1=x[1], y1=x[2], code=2, col=1)
text(x=x[1], y=x[2]+0.15, labels=expression(x))
arrows(x0=0, y0=0, x1=Ax[1], y1=Ax[2], code=2, col=2)
text(x=Ax[1], y=Ax[2]+0.15, labels=expression(paste(Ax, "=",lambda, x)), col=2)
arrows(x0=0, y0=0, x1=a[1], y1=a[2], code=2, col=3)
text(x=a[1], y=a[2]+0.15, labels=expression(a), col=3)
arrows(x0=0, y0=0, x1=Aa[1], y1=Aa[2], code=2, col=4)
text(x=Aa[1], y=Aa[2]-0.30, labels=expression(Aa), col=4)
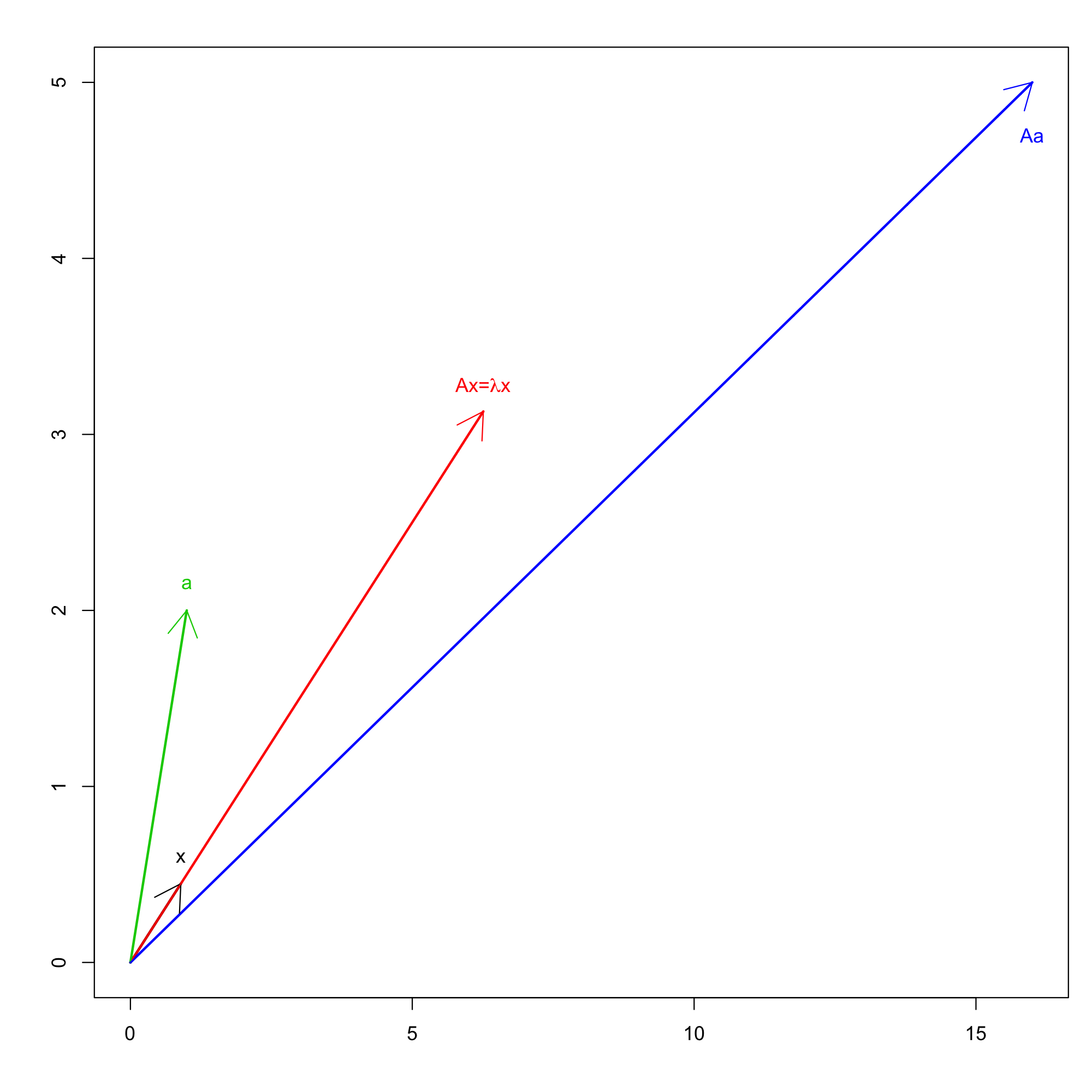
上記のコードによって出力される図は次のようになるはずだ(図1).行列\(A\)の固有ベクトル\(\boldsymbol x\)が変換\(A\)によって定数倍されている一方, 固有ベクトルではないベクトル\(\boldsymbol a\)は変換\(A\)によって異なる方向を向いていることがわかる.