EPRの論文 (in $\S$4.4)：

$\bullet$ Einstein, A., Podolosky, B. and Rosen, N.: "Can quantum-mechanical description of reality be considered completely?" Physical Review Ser 2(47), 777--780, (1935)
はいろいろな読み方のできる論文で、 「よく整理された論文」とは思えないが、 「示唆に富む論文」であることは確かと思う。 以下は、著者なりの一つの読み方である。

注意8.15 [ 量子系では、三段論法は成り立たない]



元々の EPRの論文 (in $\S$4.4) は以下のような 設定になっている． 質量$m$の同一の2つの 粒子$A_1$と$A_2$が合わさって静止しているとして， これが2つに弾けて正反対に飛び出すことを考える．



(時刻$t_1$での)粒子$A$の位置$q_A$と (時刻$t_1$での)粒子$B$の速度$v_B$ を正確に測定できる。

したがって、次の問題を得る。
$(A):$ 運動量保存則から、 (時刻$t_1$での)粒子$A$の位置$q_A$と運動量$- m v_B$ がわかるか ?
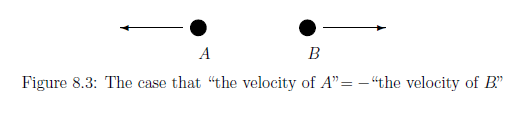
(4.3.3節で述べたように、この命題(A)が正しかったとしても, (近似同時測定に関わる定理である) ハイゼンベルグの不確定性原理(=定理4.15)と矛盾するわけではない).

さて、
  • 問題(A)は正しいか？
を以下に考える。
ここで，これを量子系の問題と考えれば,以下のようになる.

ヒルベルト空間$H_1= L^2 ({\mathbb R}_{q})$を考えて, 量子系の2粒子システム$S$をテンソルヒルベルト空間 $H =H_1 \otimes H_1 = L^2 ({\mathbb R}^2_{(q_1 , q_2{})})$ 内で議論する. 2粒子システム$S$の エンタングル状態 を ${u_0}$ $({}\in H =H_1 \otimes H_1 = L^2 ({\mathbb R}^2_{(q_1 , q_2{})}))$ $\Big($正確には, $\rho_0=| {u_0} \rangle \langle {u_0} | \Big)$ とする.　ここで,

\begin{align} {u_0} ({}q_1 , q_2{}) = \sqrt{ \frac{1}{{{ 2 \pi \epsilon \sigma} }}} e^{ - \frac{1}{8 \sigma^2 } ({}{q_1 - q_2} - 2{a} {})^2 - \frac{1}{8 \epsilon^2 } ({}{q_1 + q_2} {})^2 } \tag{8.18} \end{align}

ここで,$a \in {\mathbb R}$, 正数$\epsilon$は十分小さいとする. 各$k=1,2$に対して, $Q_k{}\! : L^2 ({\mathbb R}^2_{(q_1 , q_2{})}) \to $ $L^2 ({\mathbb R}^2_{(q_1 , q_2{})}) $ と $P_k \!: L^2 ({\mathbb R}^2_{(q_1 , q_2{})}) \to $ $L^2 ({\mathbb R}^2_{(q_1 , q_2{})})$ を次の(非有界)自己共役作用素とする.

\begin{align} & Q_1 = q_1 , \qquad P_1 = \frac{ \hbar \partial }{ i \partial q_1 } \nonumber \\ & Q_2 = q_2 , \qquad P_2 = \frac{ \hbar \partial }{ i \partial q_2 } \tag{8.19} \end{align}

ある時刻$t_0$において，次の議論を考える．

$(\sharp_1):$ (粒子$A_1$の位置, 粒子$A_2$の運動量) と 粒子$A_2$の運動量 を正確に測定して， $(x_1, p_2)$と$p'_2$ が得られたとする． もちろん， $p_2=p'_2$であるから， 例2.28[スペクトル分解]を見習って, \begin{align*} \mbox{自己共役作用素}(Q_1 \otimes P_2 ) \times (I \otimes P_2 )\mbox{ の観測量表示を} {\mathsf O}_1=({\mathbb R}^3, {\mathcal B}_{{\mathbb R}^3},F_1) \end{align*} として, \begin{align*} \underset{\text{ (粒子$A_1$の位置, 粒子$A_2$の運動量)}}{(x_1, p_2)} \;\; \underset{{\mathsf M}_{B(H)}({\mathsf O}_1,S_{[\rho_0]})}{\Longrightarrow} \;\; \underset{\text{ 粒子$A_2$の運動量}}{p_2} \end{align*} となる．
$(\sharp_2):$ また， 粒子$A_1$の運動量と 粒子$A_2$の運動量 を正確に測定して， $p_1$と$p_2$ が得られたとする． ここで， 運動量保存則から， $p_1=-p_2$ が成り立つから， \begin{align*} \mbox{自己共役作用素}(I \otimes P_2 ) \times (P_1 \otimes I ) \mbox{ の観測量表示を} {\mathsf O}_2=({\mathbb R}^2, {\mathcal B}_{{\mathbb R}^2},F_2) \end{align*} として, \begin{align*} \underset{\text{ 粒子$A_2$の運動量}}{p_2} \;\; \underset{{\mathsf M}_{B(H)}({\mathsf O}_2,S_{[\rho_0]})}{\Longrightarrow}\;\; \underset{\text{ 粒子$A_1$の運動量}}{- p_2} \end{align*} となる.
$(\sharp_3):$ したがって， $(\sharp_1)$ と $(\sharp_2)$ により， "三段論法"によって， \begin{align*} \qquad \quad \underset{\text{ 粒子$A_1$の運動量}}{- p_2} \qquad \Big( すなわち， 「\text{粒子$A_1$の運動量は，$-p_2$である}」 \Big) \end{align*} と結論できて，粒子$A_1$の位置$x_1$と 運動量$-p_2$を正確に知り得たことになる.
というような「三段論法の議論」が成立しそうであるが，
  • 結論的には，これ(=問題(A))は正しくない.
なぜならば,
$(\sharp_4):$ $ (Q_1 \otimes P_2 ) \times (I \otimes P_2 ) $と $(I \otimes P_2 ) \times (P_1 \otimes I )$ ( したがって, ${\mathsf O}_1$ と ${\mathsf O}_2$ ) は非可換で, 同時観測量が存在しないからで, そうならば,
  • $(\sharp_3)$を検証する術がない
からである

よって、 EPR論文は、
  • 量子系では、三段論法が成立しない
と主張しているとも読める。


注意8.16

EPRの論文 はかなり一般的な設定で 書かれていて， この 「三段論法の不成立」や「光より速い何かがあるのか？(非局所性の問題)」以外の問題意識 (たとえば， 「実在とは何か？」等)が主となっていて， いろいろな観点から読める論文であるが， 本書 ---言語的科学観 ---では，「実在とは何か？」には関わらない．

「三段論法の不成立」は,意外なことであるが,あってはならないことではない.


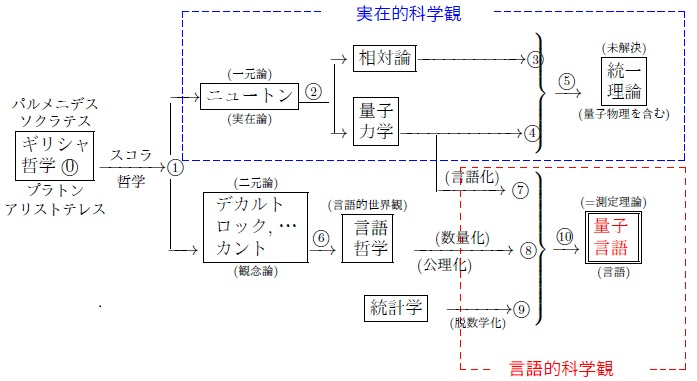
$\qquad \qquad \qquad$ Fig.1.1: 世界記述の発展史

一方、 「超光速(非局所性)」は非常に困るわけで,これはあってはならないことで,「真のパラドックス」であるが,これは量子力学が発見された当初から問題視されたことで(たとえば,ド・ブロイのパラドックス(cf.2.10節)),EPR論文で最初に指摘されたことではない. もちろん、　これは右図の⑤で解決されるべきことである。

EPR論文は、いろいろと考えさせられる示唆に富んだ論文であるが、

  • エンタングル状態の不思議さを訴えている

だけで、これ以上のことを主張しているとは思えない。 この不思議さを根底から打破するには、アインシュタイン級の天才が必要で、 そういう状況は滅多にあるわけではないので、常識的には、
  • "Stop being bothered"
として、エンタングル状態の応用を追究した方が賢いだろう。 「超光速(非局所性)」が、「超光速通信を実現しないという証明」があるらしいが、「不可能証明」 をチェックする能力は著者にはない。「瞬間移動の不可能証明」などいくらでもできそうだが、それが可能なのだから、 不可能証明は単純でない。