この節は、次の論文からの抜粋である:
量子言語の必然性がよくわかる例(ベルの不等式と射影公準)なので、上級者ならば、以下を読む前にこの論文を先に読んだ方が手っ取りばやい。
著者は「ベルの議論」を評価していない、というより、著者は「ベルの議論」の科学的意義がわかっていない。すなわち、「ベルの仕事」が無かったとしても困る科学者はいないと思っている。哲学者は多少困るかもしれないが、
そうならば、量子基礎論の分野の仕事には、過大評価・過小評価がつきものかもしれない。
確実な偉業は、「フォン・ノイマンの仕事」と「エンタングル状態($\approx$超光速)の応用」だけかもしれない。
まず、ベルの不等式の数学の部分を説明する。
次の三つのステップ(I$\sim$III)を用意する.
[Step I]:
一般基本構造$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$を考える.
測定値空間を
$X^2=\{-1,1\}^2
=
\{
(1,1),
(1,-1),
$
$
(-1,1),
$
$
(-1,-1)
\}$とする.
二つの複素数
$a= {\alpha}_1 +{\alpha}_2{}{\sqrt{-1}} $
と
$b= {}{\beta}_1 +{\beta}_2{}{\sqrt{-1}}$
は絶対値が1とする. すなわち,
$| a |$
$\equiv$
$\sqrt{{}| \alpha_1 |^2 + | {\alpha}_2 |^2{}} =1$
and
$| b |$
$\equiv$
$\sqrt{{}| \beta_1 |^2 + | {\beta}_2 |^2{}} =1$.
確率空間
$( X^2, {\cal P}(X^2), \nu_{ab})$
を次のように, 定義する:
相関関数$P(a,b)$
は以下のようになる:
これを、次のステップ [II]で答えよう.
(i):
量子系の場合
[${\cal A}=B({\mathbb C}^2) \otimes B({\mathbb C}^2)
=B({\mathbb C}^2 \otimes {\mathbb C}^2)$
]
とおく.
各 $c \in \{a,b\}$
に対して, $B({}{\mathbb C}^2{}) $内の
観測量
${\mathsf O}_c$
$\equiv$
$\bigl(X ,{\cal P}(X) , G_c \bigl)$
を次のように定める:
さらに, ニ粒子の量子系を
${ B }({\mathbb C}^2 \otimes {\mathbb C}^2{})$
内で以下のように考える.
さて, 状態
$\rho_s$
$= | {\psi_s} \rangle \langle {\psi_s} |$
と
$\rho_0$
$= | {\psi_0} \rangle \langle {\psi_0} |$
$\bigl({}\in
{\frak S}^p({}
{ B }({\mathbb C}^2 \otimes {\mathbb C}^2{})^*{})
\bigl)$
を考えよう.
ここに,
$\psi_s=(e_1\otimes e_2 -e_2\otimes e_1)/{\sqrt{2}}$
と
$\psi_0=e_1\otimes e_1$.
とする.
ユニタリ作用素
$U$
$( \in B({\mathbb C}^2 \otimes {\mathbb C}^2)$
が
$U\psi_0 =\psi_s$
を満たすとしよう.
$B({}{\mathbb C}^2 \otimes {\mathbb C}^2{})$
内の
観測量
${\mathsf O}_{ab} $
$=$
$({}X^2 , {\cal P}({}X^2{}) , F_{ab}:=
U^* (G_a \otimes G_b)U {})$
と考えて,
測定
${\mathsf M}_{B({}{\mathbb C}^2 \otimes {\mathbb C}^2{})}
({}{\mathsf O}_{ab} ,S_{[{}\rho_0{}]}{})$
を得る.
これは, 明らかに問題(D)を満たす.
なぜならば,
各$(x_1,x_2) \in X^2$に対して, 次を計算すればよい.
(ii):古典系の場合
[${\cal A}=C_0(\Omega) \otimes C_0(\Omega)=C_0(\Omega \times \Omega)$]
$\omega_0 (=(\omega_0', \omega''_0)) \in \Omega \times \Omega$,
と
$\rho_0 = \delta_{\omega_0} $
($\in
{\frak S}^p ({}{C_0(\Omega \times \Omega)}^*)$
)
考える.
$C_0(\Omega \times \Omega)$内の
観測量
${\mathsf O}_{ab}:=( X^2, {\cal P}(X^2), F_{ab})$
を次を満たすように定める:
$
[ F_{ab}( \{(x_1,x_2)\} )](\omega_0 )
=
\nu_{ab}
( \{(x_1,x_2)\} )$.
したがって,
測定
${\mathsf M}_{L^\infty (\Omega\times \Omega)}
({}{\mathsf O}_{ab} ,S_{[{}\delta_{\omega_0}{}]}{})$
を得る.
これは, 明らかに問題(D)を満たす.
[1]: S. Ishikawa, “Bell's inequality should be reconsidered in quantum language,Journal of Quantum Information Science,” Vol. 7 No. 4, 2017, pp. 140-154. doi: 10.4236/jqis.2017.74011 ( download free)
「高尚らしいこと」は疑った方がよい。
4.5.1: 古典システムにおいても"ベルの不等式"は破られる?
$(\sharp)$
$ \qquad \qquad $量子力学には、「光より速い何か」がある
という驚くべき事実がある。しかし、このことは量子力学の創成期からだれが言うともなく知られていたことと思う
(cf. ド・ブロイのパラドックスというとしても、ド・ブロイ以前にも知られていたことと思う)。
こういう歴史の中で、「EPR」や「Bell」の重要さの意味づけは混乱していると思う。
著者の意見は、
$(\flat_1)$
最大級に不可解な事実$(\sharp)$の発見者が「詠み人知らず」では困るので、アインシュタインの名前が使われた。
そして、もうすこし手の込んだトリックとして、隠れた変数に関連してBellの不等式が使われた
のだと思っている。
すなわち、
$(\flat_2)$
最大級に不可解な事実$(\sharp)$に対する「驚きの象徴」として、「EPR」や「Bell」がある。
と考える。ただし、隠れた変数の議論を過大視しないのならば、「Bell」の議論は割り引いて考えてもよい。
証明:
証明は, 簡単で,
\begin{align*}
&
|C_{13}-C_{14}|+|C_{23}+C_{24}|
\\
\le
&
\int_Y f_1(y) \cdot |f_3(y)-f_4(y)| \mu(dy)
+
\int_Y f_2(y) \cdot |f_3(y)+f_4(y)| \mu(dy)=2
\end{align*}
$(C):$
実は, 著者はベルの不等式と量子力学との関係をよく理解しているわけではないが,
一応,この節で議論しておく.
前節の議論
(EPR-パラドックス)をすこし発展させる.
$\quad$
次を満たす測定
${\mathsf M}_{\overline
{\mathcal A}
}
({\mathsf O}_{ab}:=( X^2,$
$ {\cal P}(X^2),$
$ F_{ab}) ,$
$S_{[\rho_0]}{})$
を見つけよ:
\begin{align*}\nu_{ab} (\Xi)= \rho_0( F_{ab} (\Xi))
\;\;
\quad
(\forall \Xi \in {\cal P}(X^2))
\end{align*}
[Step: II]:
問題(D)
を二つの場合,
すなわち,
について, 答える.
$\quad$
$
\begin{cases}
\mbox{(i):量子系の場合
[${\cal A}=B({\mathbb C}^2 \otimes {\mathbb C}^2)$]
}
\\
\\
\mbox{(ii):古典系の場合
[${\cal A}=C_0(\Omega \times \Omega)$]
}
\end{cases}
$
さて,
\begin{align}
e_1=
\left[\begin{array}{l}
1
\\
0
\end{array}\right],
\quad
e_2=
\left[\begin{array}{l}
0
\\
1
\end{array}\right]
\quad
(\in {\mathbb C}^2 ).
\end{align}
[Step III]:
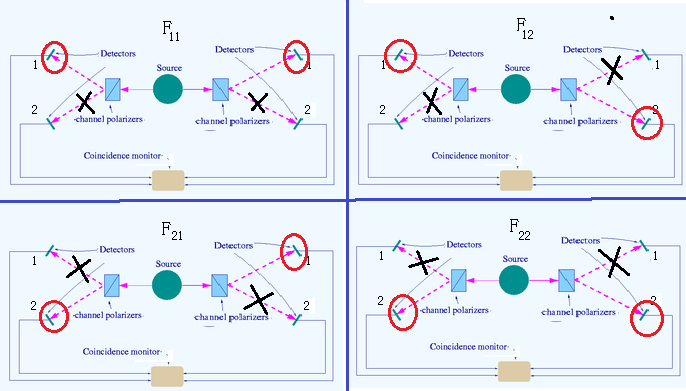
各
$k=1,2$
に対して,
絶対値1の複素数
$a^k
(=\alpha_1^k+\alpha_2^k{\sqrt{-1}} )$
と
$b^k(=\beta_1^k+\beta_2^k{\sqrt{-1}})$
を考える. ここに,
$| a^k |=| b^k |=1$に注意せよ.
さて,
テンソル
$W^*$代数
$ \otimes_{{}_{i,j=1,2}} \overline{\mathcal A} $
内の
並行測定
$\otimes_{i,j=1,2}$
${\mathsf M}_{
{\cal A}
}
({\mathsf O}_{a^ib^j}:=( X^2, {\cal P}(X^2), F_{a^ib^j}) ,$
$S_{[\rho_0]}{})$
を考えて, その測定値を
$x (\in X^8)$
とする.
すなわち,
\begin{align*}
x
&
=
\big({}
({}x_{1}^{11} , x_{2}^{11}{}),
({}x_{1}^{12} , x_{2}^{12}{}),
({}x_{1}^{21} , x_{2}^{21}{}),
({}x_{1}^{22} , x_{2}^{22}{})
\big)
\\
&
\in
{{{\times}}}_{i,j=1,2} X^2
\end{align*}
ここで, (4.50)により,
各
$i,j=1,2$
に対して, 次を得る:
\begin{align*}
P({a^{i},b^{j}})
&
=
\!\!\!
\sum_{(x^{ij}_1, x^{ij}_2) \in X\times X }
\!\!\!
x^{ij}_1 \cdot x^{ij}_2 \rho_0 (F_{a^ib^j}( \{(x^{ij}_1,x^{ij}_2)\} ))
\\
&
=
-\alpha^{i}_1 \beta^{j}_1 - \alpha^{i}_2 \beta^{j}_2
\end{align*}
ここで, 次のようにおいて,
\begin{align*}
a^1 ={\sqrt{-1}},
\;
b^1 = \frac{1+{{\sqrt{-1}}}}{ \sqrt{2} },
\;
a^2 = 1,
\;
b^2 = {}\frac{1-{{\sqrt{-1}}}}{ \sqrt{2} },
\end{align*}
次の計算を得る.
\begin{align}
|P({}a^1 , b^1{}) - P({}a^1 , b^2{})|
\;
+
\;
|P({}a^2 , b^1{}) + P({}a^2 , b^2 {})|
=
2 \sqrt{2}
\tag{4.51}
\end{align}
二つの場合
(
i.e.,
量子系の場合
[${\cal A}=B({\mathbb C}^2 \otimes {\mathbb C}^2)$]
と古典系の場合
[${\cal A}=C_0(\Omega\times \Omega)$])で,
式(4.51)が成立することになる.
もちろん,これが「超光速(=非局所性=遠隔作用)」
を示唆していることはわかるが,「超光速」はド・ブロイのパラドックスの時点
(または,もっと以前の量子力学提唱時点)でわかっていることで,
したがって,
| $(E):$ | いまさら, 何なの? |
そうだとしても、
また、
ただ、習慣的に、
という。
「光より速い何か」があるとしても、それによって、「超光速通信」が可能かどうかは未定である。 一応、「不可能証明」がされていることになっているが、物理の中の不可能証明のチェックは容易ではないので、 著者はチェックし切れていない。
4.5.2: 悩むのはやめよう(Stop being bothered)
こう言った方が公平と思うが,ほとんどの物理学者は悩んでいない(
by Mermin).

| $\bullet$ | 「(ファインマンの問い掛け(第1章の冒頭)):本当の問題はない」からスタートすれば,広大なニューフロンテアが開ける。 古典系も含むわけで,単純に言って,2倍になる |
| $\bullet$ | 量子言語から,始めれば,本当の問題は消去される |
いろいろな意見があるかもしれないが, 天才でなければ,「本当の問題はない」と信じた方が幸せになれる. これは, 偏った意見ではないと考える. 事実,大抵の量子力学の本では,「ベルの不等式,エンタングルメント」の 深淵さを強調するが,それ以上突き進むことはしないで (すなわち,「本当の問題はない」として),さらに言い換えると,
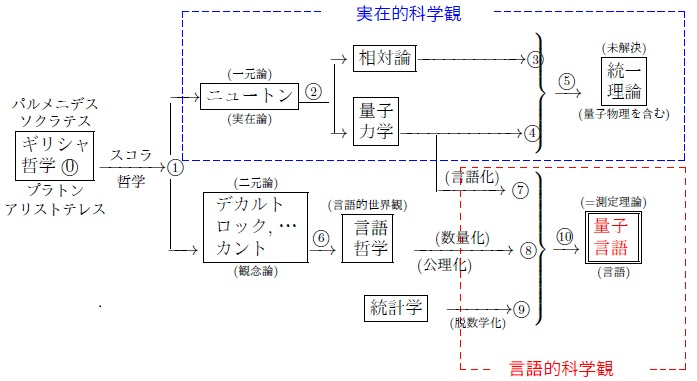
である。
しかし、
あなたが天才で、しかも悩みたいならば、
主張1.1(in $\S$1.1)の
右図の⑤で悩もう
である。