20.1 Two kinds of ( realistic and linguistic ) world- views
In this lecture note, we assert the following figure:
Most physicists
feel that
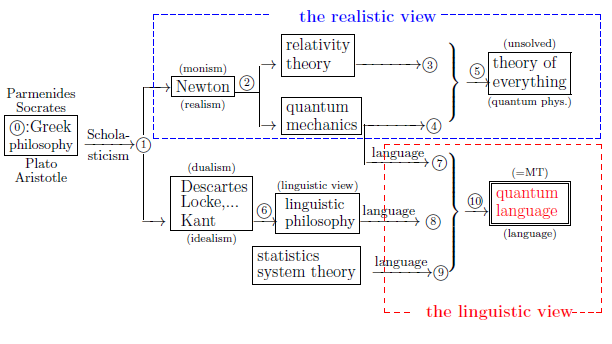
And they want to unify the two aspects.
However,
quantum language asserts that
$(A_1):$
quantum mechanics has both realistic aspect and
metaphysical aspect.
In this lecture, I assert that quantum language, roughly speaking, has the three aspects as follows.
$(A_2):$
Two aspects are separated, and
they develop in the respectively different directions
$⑤$
and
$⑩$
in Figure 20.1.
20.1 Postscript: Two kinds of ( realistic and linguistic ) world- views
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
