Abstract (14.0: Realized causal observable in classical systems )
Abstract:
As mentioned in the previous chapters,
what is important
is
In this chapter,
we discuss the relationship more systematically.
That is, we add the further argument concerning
the realized causal observable.
This field is too vast, thus, we mainly concentrate our interest to
classical systems, particularly, Zeno's paradox.
That is,
$\bullet$
to exercise the relationship of
measurement and causality

We believe that this is the final answer to Zeno's paradox.
$(\flat):$
to describe
the flying arrow ( the best work in Zeno's paradoxes )
in terms of quantum language
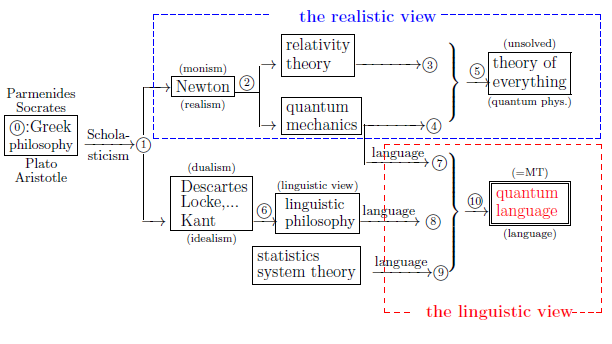
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to
assert the following figure 1.1:
14.0: Realized causal observable in classical systems
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
