Let ${\mathbb C}^2$ be the two dimensional Hilbert space,
i,e.,
${\mathbb C}^2$
$=$
$
\Big\{
\left[\begin{array}{l}
z_1
\\
z_2
\\
\end{array}\right]
\;|
\;
z_1, z_2 \in {\mathbb C}
\Big\}$.
And put
Here,
define the {observable
${\mathsf O}_x=(\{-1, 1 \}, 2^{\{-1, 1 \}}, F_x )$
in
$B({\mathbb C}^2)$}
such that
Here, note that
Let $H$ be a Hilbert space such that
$L^2({\mathbb R})$.
And {let ${\mathsf O}=(X, {\mathcal F}, F )$
be an observable in $B(H)$}.
For example, consider the position observable,
that is,
$X={\mathbb R}$,
${\mathcal F}={\mathcal B}_{{\mathbb R}}$,
and
Let
$u_1$
and $u_2$
$( \in H)$ be orthonormal elements,
i.e.,
$\| u_1 \|_H=\| u_2 \|_H=1$
and
$\langle u_1 , u_2 \rangle =0$.
Put
where $\alpha_i \in {\mathbb C}$
such that
$| \alpha_1|^2 + |\alpha_2|^2=1$.
Furthermore, define $\psi \in {\mathbb C}^2 \otimes H $
$($
the tensor Hilbert space of ${\mathbb C}^2$ and $H$)
such that
where $\alpha_i \in {\mathbb C}$
such that
$| \alpha_1|^2 + |\alpha_2|^2=1$.
11.7.2: Interference
where
the
interference term
(i.e.,
the third term)
appears.
Then, by the interference term (i.e.,
$2
\mbox{[Real part]}
(
\overline{\alpha}_1\alpha_2
\langle
u_1 ,
F(\Xi)u_2
\rangle
)$
),
we get the following graph.
11.7: quantum eraser experiment
Let us explain
quantum eraser experiment.
This section is extracted from
$(\sharp):$
S. Ishikawa,
The double-slit quantum eraser experiments and Hardy's paradox in the quantum linguistic interpretation,
arxiv:1407.5143[quantum-ph],( 2014)
11.7.1: Tensor Hilbert space
Consider the measurement:
\begin{align}
{\mathsf M}_{B({\mathbb C}^2 \otimes H )}
({\mathsf O}_x \otimes {\mathsf O} , S_{[| \psi \rangle \langle \psi |]} )
\tag{11.27}
\end{align}
Then, we see:
\begin{align}
&
\langle
\psi,
(F_x(\{ 1 \}) \otimes F(\Xi) )
\psi
\rangle
\\
=
&
\langle
\alpha_1 e_1 \otimes u_1 + \alpha_2 e_2 \otimes u_2,
(F_x(\{ 1 \} \otimes F(\Xi) ))
(
\alpha_1 e_1 \otimes u_1 + \alpha_2 e_2 \otimes u_2
)
\rangle
\\
=
&
\frac{1}{2}
\langle
\alpha_1 e_1 \otimes u_1 + \alpha_2 e_2 \otimes u_2,
\alpha_1 (e_1+e_2) \otimes F(\Xi) u_1 + \alpha_2 (e_1+ e_2) \otimes F(\Xi) u_2
\rangle
\\
=
&
\frac{1}{2}
\Big(
|\alpha_1|^2
\langle
u_1 ,
F(\Xi)u_1
\rangle
+
|\alpha_2|^2
\langle
u_2 ,
F(\Xi)u_2
\rangle
+
\overline{\alpha}_1\alpha_2
\langle
u_1 ,
F(\Xi)u_2
\rangle
+
{\alpha}_1 \overline{\alpha}_2
\langle
u_2 ,
F(\Xi)u_1
\rangle
\Big)
\\
=
&
\frac{1}{2}
\Big(
|\alpha_1|^2
\langle
u_1 ,
F(\Xi)u_1
\rangle
+
|\alpha_2|^2
\langle
u_2 ,
F(\Xi)u_2
\rangle
+
2
\mbox{[Real part]}
(
\overline{\alpha}_1\alpha_2
\langle
u_1 ,
F(\Xi)u_2
\rangle
)
\Big)
\end{align}
$(A_1):$
the probability that a measured value
$(1, x ) (\in \{-1,1\} \times X )$
belongs to
$
\{1\} \times \Xi $
is given by
Define the probability density function $p_1$ by
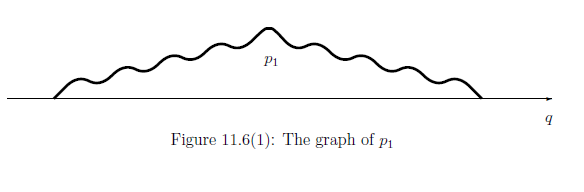
Also, we see:
| $(A_2):$ | the probability that a measured value $(-1, x ) (\in \{-1,1\} \times X )$ belongs to $ \{-1\} \times \Xi $ is given by |
where the interference term (i.e., the third term) appears. Define the probability density function $p_2$ by
\begin{align} \int_\Xi p_2 (q) dq =\frac{\langle \psi, (F_x(\{- 1 \}) \otimes F(\Xi) ) \psi \rangle}{\langle \psi, (F_x(\{ -1 \}) \otimes I ) \psi \rangle} \quad (\forall \Xi \in {\mathcal F} ) \end{align} Then, by the interference term (i.e., $-2 \mbox{[Real part]} ( \overline{\alpha}_1\alpha_2 \langle u_1 , F(\Xi)u_2 \rangle )$ ), we get the following graph.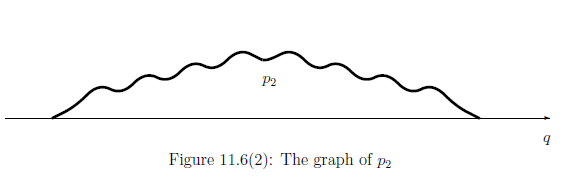
Consider the measurement: \begin{align} {\mathsf M}_{B({\mathbb C}^2 \otimes H )} ({\mathsf O}_x \otimes {\mathsf O} , S_{[| \psi \rangle \langle \psi |]} ) \tag{11.29} \end{align} Then, we see
| $(A_3):$ | the probability that a measured value $(u, x ) (\in \{1, -1\} \times X )$ belongs to $ \{1,-1\} \times \Xi $ is given by |
Define the probability density function $p_3$ by \begin{align} \int_\Xi p_3 (q) dq = \langle \psi, (I \otimes F(\Xi) ) \psi \rangle \quad (\forall \Xi \in {\mathcal F} ) \end{align}
Since there is no interference term, we get the following graph.
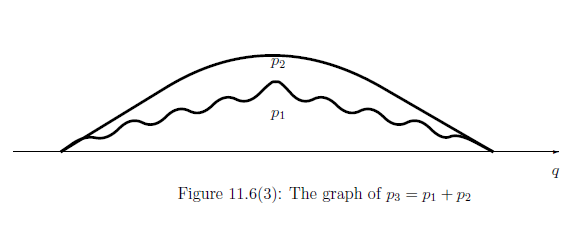
Remark 11.17
Note that \begin{align} \underset{\mbox{no interference}}{\fbox{(A$_3$)}} = \underset{\mbox{interferences are canceled}}{\fbox{(A$_1$)+(A$_2$)}} \end{align}
