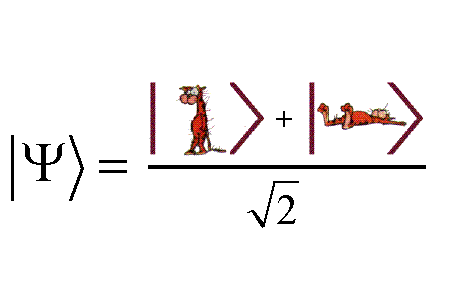11.5: Schrödinger's cat,
Wigner's friend and Laplace's demon
11.5.1: Schrödinger's cat and Wigner's friend
Let us explain Schrödinger's cat paradox
in
the Schrödinger picture.
Problem 11.14 [Schrödinger's cat]
| $(a):$ |
Suppose we put a cat in a cage with a radioactive atom, a Geiger counter,
and a poison gas bottle; further suppose that the atom
in the cage has a half-life of one hour,
a fifty-fifty chance of decaying within the hour.
If the atom decays, the Geiger counter will tick;
the triggering of the counter will
get the lid off the poison gas bottle, which will kill the cat.
If the atom does not decay, none of the above things happen,
and the cat will be alive.
|
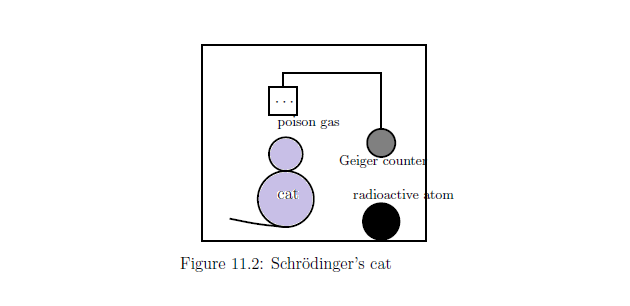
Here, we have the following question:
| $(b):$ |
Asuume that, after one hour, you look at the inside of the box.
Then,
do you know whether
then
the cat is dead or alive after one hour,
(= $60^{60}$ seconds ) ?
Of course, we say that it is half-and-half whether the cat is alive.
However, our problem is
Clarify the meaning of "half-and-half"
|
| $\fbox{Note 11.1}$ |
[Wigner's friend]:
Instead of the above (b), we consider as follows.
| $(b)':$ |
after one hour,
Wigner's friend look at the inside of the box,
and thus, he know
whether
the cat is dead or alive after one hour,
(= $60^{60}$ seconds ).
And further,
after two hours,
Wigner's friend informs you the fact.
How is the cat?
|
This problem is not difficult.
That is because
the linguistic interpretation says that
"the moment you measured"
is out of the description of quantum language.
Recall the spirit of the linguistic world-view
(i.e.,
Wittgenstein's words)
such as
\begin{align}
\color{magenta}{\mbox{
The limits of my language mean the limits of my world}}
\end{align}
and
\begin{align}
\color{magenta}{\mbox{
What we cannot speak about we must pass over in silence.
}}
\end{align}
|
11.5.2: The usual answer without quantum language
Answer 11.15 [The ordinary answer to Problem11.14(i.e.,
the answer without quantum language)].
Put
${\mathbf q}=(q_{11}, q_{12}, q_{13}, q_{21},q_{22}, q_{23}, \dots, q_{n1},q_{n2}, q_{n3} ) \in {\mathbb R}^{3n} $.
And put
\begin{align}
\nabla_i^2
=
\frac{\partial^2}{\partial q_{i1}^2}
+
\frac{\partial^2}{\partial q_{i2}^2}
+
\frac{\partial^2}{\partial q_{i3}^2}
\end{align}
Consider the quantum system basic structure:
\begin{align}
[{\mathcal C}(H)
\subseteq
B(H)
\subseteq
B(H)]
\qquad
\mbox{
(
where,$H=L^2 ( {\mathbb R}^{3n}, d {\mathbf q} )$
)}
\end{align}
And consider the Schrödinger equation (concerning $n$-particles system):
\begin{align}
\left\{\begin{array}{ll}
i \hbar \frac{\partial}{\partial t} \psi ( {\mathbf q}, t )
=
\Big[
\sum_{i=1}^n \frac{- \hbar^2}{2m_i} \nabla_i^2 + V( {\mathbf q}, t )
\Big]
\psi ( {\mathbf q}, t )
\\
\\
\psi_0({\mathbf q})=\psi ( {\mathbf q}, 0 ):
\mbox{initial condition}
\end{array}\right.
\tag{11.24}
\end{align}
where,$m_i$ is the mass of a particle $P_i$,
$V$ is a potential energy.
If we believe in quantum mechanics,
it suffices to solve
this Schrödinger equation
(11.24).
That is,
| $(A_1):$ |
Assume that
the wave function
$\psi( \cdot, 60^2 )=U_{0,60^2} \psi_0$
after one hour
(i.e.,
$60^2$ seconds)
is calculated.
Then, the state $\rho_{60^2}$
$(\in {\mathcal Tr}_{+1}^p (H)
)$ after $60^2$ seconds
is represented by
\begin{align}
\rho_{60^2}=
|
\psi_{60^2}
\rangle
\langle
\psi_{60^2}
|
\tag{11.25}
\end{align}
(where,
$
\psi_{60^2}
=
\psi(\cdot , 60^2 )
$).
|
Now,
define the observable ${\mathsf O}=
(X=\{\mbox{life}, \mbox{death}\},
2^X, F)$
in
$B(H)$
as follows.
| $(A_2):$ | that is,putting
\begin{align}
&
V_{\mbox{life}} (\subseteq H )
=
\Big\{ u\in H \;|\; "\mbox{ the state } \frac{|u\rangle \langle u |}{\|u\|^2}" \Leftrightarrow
\mbox{"cat is alive"}
\Big\}
\\
&
V_{\mbox{death}} (\subseteq H )=\mbox{the orthogonal complement space of }V_{\mbox{life}}
\\
&
\qquad
\qquad
\qquad
= \{ u \in H \;|\; \langle u, v \rangle = 0 \;\;(\forall
v \in V_{\mbox{life}} )
\}
\end{align}
define
$F(\{\mbox{life}\})(\in B(H) )$
is the projection of the closed subspace $V_{\mbox{life}}$
and
$F(\{\mbox{death}\})=I - F(\{\mbox{life}\})$,
|
Here,
| $(A_3):$ |
consider the measurement ${\mathsf M}_{B(H)}({\mathsf O}=(X, 2^X, F), S_[\rho_{60^2]})$.
The probability that a measured value
$
\left[\begin{array}{ll}
\mbox{life}
\\
\mbox{death}
\end{array}\right]
$
is obtained is given by
\begin{align}
\left[\begin{array}{ll}
{}_{{\mathcal Tr}(H)}
\Big(\rho_{60^2}, F(\{\mbox{life}\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{\mbox{life}\})\psi_{60^2} \rangle=0.5
\\
{}_{{\mathcal Tr}(H)}
\Big(\rho_{60^2}, F(\{\mbox{death}\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{\mbox{death}\})\psi_{60^2} \rangle=0.5
\end{array}\right]
\end{align}
|
Therefore,we can assure that
\begin{align}
&
\psi_{60^2}= \frac{1}{\sqrt 2}( \psi_{\mbox{life}}+ \psi_{\mbox{death}})
\tag{11.26}
\\
(\mbox{where, }
&
\psi_{\mbox{life}}\in V_{\mbox{life}},\|\psi_{\mbox{life}}\|=1
\quad
\psi_{\mbox{death}}\in V_{\mbox{death}},\|\psi_{\mbox{death}}\|=1
)
\nonumber
\end{align}
Hence, we can conclude that
| $(A_4):$ |
the state (or, wave function) of the cat (after one hour )
is represented by
(11.26),
that is,
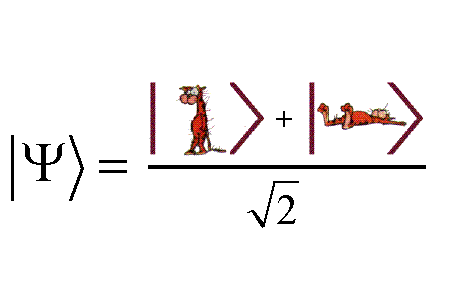 $
\frac{
\mbox{"Fig. $(\sharp_1)$"} + \mbox{ "Fig. ($\sharp_2$)"}
}{\sqrt{2}}
$
$
\frac{
\mbox{"Fig. $(\sharp_1)$"} + \mbox{ "Fig. ($\sharp_2$)"}
}{\sqrt{2}}
$
|
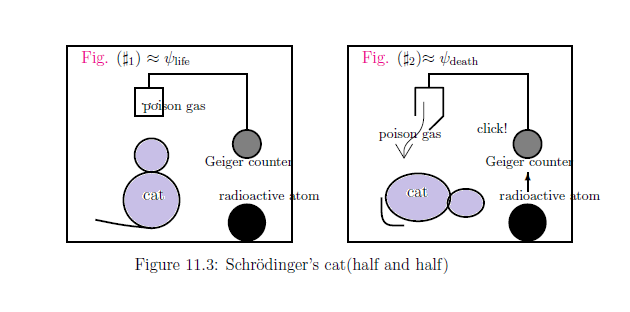 And,
And,
| $(A_5):$ |
After one hour (i.e,
to the moment of opening a window),
It is decided "the cat is dead" or "the cat is vigorously alive."
That is,
\begin{align}
&
\mbox{"half-dead"}
\Big(=\frac{1}{2}(|\psi_{\mbox{life}}+ \psi_{\mbox{death}}\rangle \langle \psi_{\mbox{life}}+ \psi_{\mbox{death}}|)\Big)
\\
&
\xrightarrow[{\mbox{ the collapse of wave function}}]{{
\mbox{
to the moment of opening a window
}}}
\left\{\begin{array}{ll}
\mbox{"alive"} (=|\psi_{\mbox{life}}\rangle \langle \psi_{\mbox{life}}|)
\\
\\
\mbox{"dead"} (=|\psi_{\mbox{death}}\rangle \langle \psi_{\mbox{death}}|)
\end{array}\right.
\end{align}
|
$\square \quad$
11.5.3: The quantum linguistic answer
 Answer 11.16 [The quantum linguistic answer to Problem11.14]
Answer 11.16 [The quantum linguistic answer to Problem11.14]
In quantum language,
the quantum decoherence
is permitted.
That is,
we can assume that
| $(B_1):$ |
the state $
\rho'_{60^2}
$
after one hour
is represented by
the following mixed state
\begin{align}
\rho'_{60^2}
=
\frac{1}{2}
\Big(
|
\psi_{\mbox{life}}
\rangle
\langle
\psi_{\mbox{life}}
|
+
|
\psi_{\mbox{death}}
\rangle
\langle
\psi_{\mbox{death}}
|
\Big)
\end{align}
That is,
we can assume
the decoherent causal operator
$\Phi_{0, 60^2}: B(H) \to B(H)$
such that
\begin{align}
(\Phi_{0, 60^2})_* ( \rho_0)
=
\rho'_{60^2}
\end{align}
|
Here,consider the
measurement
${\mathsf M}_{B(H)}({\mathsf O}=(X, 2^X, F), S_[\rho'_{60^2}])$,
or, its Heisenberg picture
${\mathsf M}_{B(H)}(\Phi_{0, 60^2}{\mathsf O}=(X, 2^X, \Phi_{0, 60^2}F), S_[\rho'_{0}])$. Of course we see:
| $(B_2):$ |
The probability that a measured value
$
\left[\begin{array}{ll}
\mbox{life}
\\
\mbox{death}
\end{array}\right]
$
is obtained by
the measurement
\\
${\mathsf M}_{B(H)}(\Phi_{0, 60^2}{\mathsf O}=(X, 2^X, \Phi_{0, 60^2}F), S_[\rho'_{0}])$
is given by
\begin{align}
\left[\begin{array}{ll}
{}_{{\mathcal Tr}(H)}
\Big(\rho_{0}, \Phi_{0, 60^2}F(\{\mbox{life}\}) \Big){}_{B(H)}=\langle
\psi'_{60^2},F(\{\mbox{life}\})\psi_{60^2} \rangle=0.5
\\
{}_{{\mathcal Tr}(H)}
\Big(\rho_{0}, \Phi_{0, 60^2}F(\{\mbox{death}\}) \Big){}_{B(H)}=\langle
\psi'_{60^2},F(\{\mbox{death}\})\psi_{60^2} \rangle=0.5
\end{array}\right]
\end{align}
|
Also,"the moment of measuring" and "the collapse of wave function"
are prohibited in the linguistic interpretation,
but the statement
(B$_2$)
is within quantum language.
$\square \quad$
11.5.4: Summary (Laplace's demon)
Summary 11.17 [Schrödinger's cat in quantum language]
Here,
let us examine
Answer11.15
:(A$_5$)
v.s.
Answer11.16
:(B$_2$)
| $(C_1):$ |
the answer (A$_5$) may be unnatural,
but
it is
an argument which cannot be confuted,
|
On the other hand,
| $(C_2):$ |
the answer (B$_2$) is natural.
but the non-deterministic time evolution is used.
|
Since the non-deterministic causal operator
(i.e.,
quantum
decoherence)
is permitted in quantum language,
we conclude that
| $(C_3):$ |
Answer11.16:(B$_2$)
is superior to
Answer11.15:(A$_1$)
|
For the reason that
the non-deterministic causal operator
(i.e.,
quantum
decoherence)
is permitted in quantum language,
we add the following.
| $\bullet$ |
If Newtonian mechanics is applied to the whole universe, Laplace's demon
appears.
Also,
if Newtonian mechanics is applied to the microworld,
chaos appears.
This kind of supremacy of physics is not natural, and thus, we consider that
these are out of "the limit of Newtonian mechanics"
|
And,
| $\bullet$ |
when we want to apply Newton mechanics to phenomena
out of
"the limit of Newtonian mechanics",
we often use the stochastic differential equation
(and
Brownian motion).
This approach is called "dynamical system theory",
which is not physics but
metaphysics.
\begin{align}
&
\underset{\mbox{ physics}}{
\fbox{Newtonian mechanics}
}
\xrightarrow[\mbox{linguistic turn}]{\mbox{out of the limits}}
\underset{\mbox{ metaphysics}}{
\fbox{dynamical system theory; statistics}
}
\\
&{}
\end{align}
|
In the same sense,
we consider that
quantum mechanics has "the limit".That is,
| $\bullet$ |
Schrödinger's cat is out of quantum mechanics.
|
And thus,
| $\bullet$ |
When we want to apply quantum mechanics to phenomena
out of
"the limit of quantum mechanics",
we often use the quantum decoherence.
Although this approach is not physics but
metaphysics,
it is quite
powerful.
\begin{align}
\underset{\mbox{ physics}}{
\fbox{quantum mechanics}
}
\xrightarrow[\mbox{linguistic turn}]{\mbox{out of the limits}}
\underset{\mbox{ metaphysics}}{
\fbox{quantum language}
}
\end{align}
|
| $\fbox{Note 11.2}$ |
If we know
the present state of the universe
and
the kinetic equation
(=the theory of everything),
and if we calculate it,
we can know everything
(from past to future).
There may be a reason to believe this idea.
This intellect is often referred to as
Laplace's demon.
Laplace's demon is sometimes discussed as
the super realistic-view (i.e.,
the realistic-view
over which the degree passed).
 Thus, we consider the following correspondence:
\begin{align}
\underset{\mbox{ physics}}{
\fbox{Newtonian mechanics}
}
\xrightarrow[\mbox{super realistic-view}]{\mbox{out of the limits}}
\underset{\mbox{ physics?}}{
\fbox{Laplace's Demon}
}
\end{align}
This should be compared with the formula (11.19).
Thus, we consider the following correspondence:
\begin{align}
\underset{\mbox{ physics}}{
\fbox{Newtonian mechanics}
}
\xrightarrow[\mbox{super realistic-view}]{\mbox{out of the limits}}
\underset{\mbox{ physics?}}{
\fbox{Laplace's Demon}
}
\end{align}
This should be compared with the formula (11.19).
|