10.2: Causality---Mathematical preparation
10.2.1:The Heisenberg picture and the Schrödinger picture
First, let us review the general basic structure
(cf. $\S$2.1.3
)
as follows.
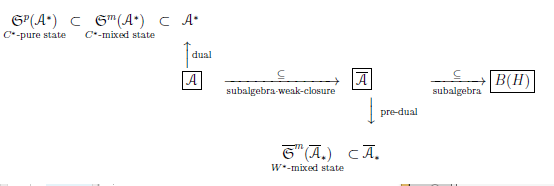
Consider the basic structure
$[{\mathcal A} \subseteq \overline{\mathcal A} ]_{B(H)}$.
For each
$\rho \in \overline{\mathcal A}_\ast$,
$F \in {\mathcal A} (\subseteq \overline{\mathcal A}
\subseteq B(H) )$,
we see that
Thus,we can consider that $\rho \in {\mathcal A}^*$.
That is,
in the sense of (10.3),we consider that
When $\rho (\in \overline{\mathcal A}_* )$
is regarded as the element of ${\mathcal A}^*$,
it is sometimes denoted by $\widehat{\rho}$. Therefore,
A continuous linear operator
$\Phi_{1,2}:\overline{\mathcal A}_2
\to \overline{\mathcal A}_1 $
is called a
causal operator ( or,
Markov causal operator ,
the Heisenberg picture of "causality"),
if it satisfies the following
(i)$\mbox{---}$(iv):
Remark 10.3 [$\overline{\mathcal A}_\ast \subseteq {\mathcal A}^*$]
In addition,
the causal operator
${\Phi}_{1,2}$
is called a
deterministic causal operator, if it satisfies that
\begin{align}
({\Phi}_{1,2})^* ({\frak S}^p({\mathcal A}_1^*) )
\subseteq
{\frak S}^p({\mathcal A}_2^*)
\tag{10.10}
\end{align}
(i):
$F_2 \in \overline{\mathcal A}_2 \;\; F_2 {\; \geqq \;}0$
$\Longrightarrow$
$\Phi_{12}F_2 {\; \geqq \;}0$
(ii): $ \Phi_{12} I_{\overline{\mathcal A}_2} =I_{\overline{\mathcal A}_1} $
$\qquad$
(where,$I_{\overline{\mathcal A}_1} (\in {\overline{\mathcal A}_1} )$
is the identity)
(iii):
there exists the continuous linear operator
$({\Phi}_{1,2})_*:(\overline{\mathcal A}_1)_*
\to ( \overline{\mathcal A}_2)_* $
such that
\begin{align}
&
\mbox{(a)} \quad
{}_{\stackrel{{}}{(\overline{\mathcal A}_1)_* }}\Big(\rho_1, \Phi_{1,2} F_2 \Big){}_{\stackrel{{}}{\overline{\mathcal A}_1 }}
=
{}_{\stackrel{{}}(\overline{\mathcal A}_2)_* }\Big( ({\Phi}_{1,2})_\ast \rho_1, F_2\Big){}_{\stackrel{{}}{\overline{\mathcal A}_2 }}
\qquad
(\forall \rho_1 \in (\overline{\mathcal A}_1)_*,
\forall F_2 \in \overline{\mathcal A}_2 )
\\
&\mbox{(b)} \quad
({\Phi}_{1,2})_\ast (\overline{\frak S}^m( ( \overline{\mathcal A}_1)_*) )
\subseteq
\overline{\frak S}^m((\overline{\mathcal A}_2)_*)
\tag{10.7}
\end{align}
This $({\Phi}_{1,2})_*$
is called the pre-dual causal operator
of
${\Phi}_{1,2}$.
(iv):
there exists the continuous linear operator
${\Phi}_{1,2}^*:{\mathcal A}_1^*
\to {\mathcal A}_2^*
$
such that
\begin{align}
&
\mbox{(a)} \quad
{}_{\stackrel{{}}{(\overline{\mathcal A}_1)_* }}\Big(\rho_1, \Phi_{1,2} F_2 \Big){}_{\stackrel{{}}{\overline{\mathcal A}_1 }}
=
{}_{\stackrel{{}}{\mathcal A}_2^* }\Big( {\Phi}_{1,2}^\ast \widehat{\rho}_1, F_2\Big){}_{\stackrel{{}}{{\mathcal A}_2 }}
\qquad
\tag{10.8}
\\
&
\qquad \qquad \qquad \qquad
(\forall \rho_1 = \widehat{\rho}_1 \in (\overline{\mathcal A}_1)_*
(\subseteq {\mathcal A}_1^*),
\forall F_2 \in {\mathcal A}_2 )
\nonumber
\\
&
\mbox{(b)} \quad
({\Phi}_{1,2})^* ({\frak S}^p({\mathcal A}_1^*) )
\subseteq
{\frak S}^m ({\mathcal A}_2^*)
\tag{10.9}
\end{align}
This ${\Phi}_{1,2}^*$
is called the
dual operator
of
${\Phi}_{1,2}$.
$\fbox{Note 10.3}$
[
Causal operator in Classical systems]
Consider the two basic structures:
\begin{align}
[C_0(\Omega_1) \subseteq L^\infty (\Omega_1, \nu_1 )]_{B(H_1)}
\mbox{ and }
[C_0(\Omega_2) \subseteq L^\infty (\Omega_2, \nu_2 )]_{B(H_2)}
\end{align}
A continuous linear operator $\Phi_{1,2}:L^\infty (\Omega_2)
\to L^\infty (\Omega_1) $
called
a causal operator,
if it satisfies
the following
(i)$\mbox{---}$(iv):
In addition,
a causal operator ${\Phi}_{1,2}$
is called a
deterministic causal operator,
if
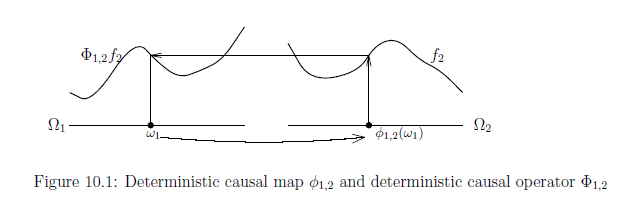
there exists a continuous map $\phi_{1,2}:\Omega_1 \to \Omega_2$
such that
\begin{align}
[\Phi_{1,2}f_2](\omega_1)
=
f_2(\phi_{1,2}(\omega_1))
\quad
(\forall f_2 \in C(\Omega_2 ), \forall \omega_1
\in \Omega_1 )
\tag{10.11}
\end{align}
This $\phi_{1,2}:\Omega_1 \to \Omega_2$
is called a
deterministic causal map.
Here, it is clear that
\begin{align}
\Omega_1
\approx
{\frak S}^p(C_0(\Omega_1)^*) \ni
\delta_{\omega_1}
\xrightarrow[\Phi_{12}^*]{} \delta_{\phi_{12}(\omega_1)}
\in
{\frak S}^p(C_0(\Omega_2)^*)
\approx
\Omega_2
\end{align}
$(i):$
$f_2 \in L^\infty (\Omega_2), \;\; f_2 {\; \geqq \;}0$
$\Longrightarrow$
$\Phi_{12}f_2 {\; \geqq \;}0$
(ii):
$\Phi_{12} 1_2 = 1_1$
where,
$1_k (\omega_k ) = 1$
$(
\forall \omega_k \in \Omega_k, k=1,2)$
(iii):
There exists a continuous linear operator $({\Phi}_{1,2})_\ast :L^1 (\Omega_1)
\to L^1_{}(\Omega_2) $
(and
$({\Phi}_{1,2})_\ast :L^1_{+1} (\Omega_1)
\to L^1_{+1}(\Omega_2) $
)
such that
\begin{align}
&
\int_{\Omega_1} [\Phi_{1,2} f_2](\omega_1) \;\;\rho_1 ( \omega_1 )
\nu_1( d \omega_1 )
=
\int_{\Omega_2} f_2(\omega_2)
\;\;
[({\Phi}_{1,2})_\ast \rho_1](\omega_2 ) \nu_2 ( d \omega_2 )
\\
& \hspace{4cm}
(\forall \rho_1 \in L^1 (\Omega_1),
\forall f_2 \in L^\infty (\Omega_2))
\end{align}
This $({\Phi}_{1,2})_\ast$
is called a
pre-dual causal operator
of
${\Phi}_{1,2}$.
(iv):
There exists a continuous linear operator ${\Phi}_{1,2}^\ast :{\mathcal M} (\Omega_1)
\to {\mathcal M}(\Omega_2) $
(and
${\Phi}_{1,2}^\ast :{\mathcal M}_{+1} (\Omega_1)
\to {\mathcal M}_{+1}(\Omega_2) $
)
such that
\begin{align}
&
{}_{\stackrel{{}}{L^1(\Omega_1) }}\Big(\rho_1, \Phi_{1,2} F_2 \Big){}_{\stackrel{{}}{L^\infty(\Omega_1) }}
=
{}_{\stackrel{{}}{{\mathcal M}(\Omega_2) }}\Big( {\Phi}_{1,2}^\ast \widehat{\rho}_1, F_2\Big){}_{\stackrel{{}}{{C_0}(\Omega_2) }}
\\
&
\qquad
(\forall \rho_1=\widehat{\rho}_1 \in {\mathcal M}(\Omega_1),
\forall F_2 \in {C_0}(\Omega_2) )
\end{align}
where,
$\widehat{\rho}_1(D)= \int_D \rho_1 ( \omega_1) \nu_1(d \omega_1)$
$(\forall D \in {\mathcal B}_{\Omega_1} )$.
This $({\Phi}_{1,2})^\ast$
is called a dual causal operator of
${\Phi}_{1,2}$.
Theorem 10.5 [Continuous map and deterministic causal map] Let $(\Omega_1, {\cal B}_{\Omega_1}, \nu_1)$ and $(\Omega_2, {\cal B}_{\Omega_2}, \nu_2)$ be measure spaces. Assume that a continuous map $\phi_{1,2}:\Omega_1 \to \Omega_2$ satisfies:
\begin{align} D_2 \in {\cal B}_{\Omega_2}, \; \; \nu_2 ( D_2 ) = 0 \quad \Longrightarrow \quad \nu_1 ( \phi_{1,2}^{-1} ( D_2 )) = 0. \end{align}Then, the continuous map $\phi_{1,2}:\Omega_1 \to \Omega_2$ is deterministic, that is, the operator ${\Phi}_{1,2} :L^{\infty} (\Omega_2, \nu_2) \to L^{\infty} (\Omega_1, \nu_1)$ defined by (10.11) is a deterministic causal operator.
Proof For each ${\overline \rho}_1$ $\in L^1(\Omega_1 , \nu_1 )$, define a measure $\mu_2$ on $(\Omega_2 , {\cal B}_{\Omega_2})$ such that
\begin{align} \mu_2 ( D_2 ) = \int_{\phi_{1,2}^{-1} ( D_2 ) } {\overline \rho}_1 (\omega_1) \; \nu_1 ( d \omega_1 ) \qquad (\forall D_2 \in {\cal B}_{\Omega_2} ) \end{align}Then, it suffices to consider the Radon-Nikodym derivative $[\Phi_{1,2}]_* ({\overline \rho}_1) = {d \mu_2}/{d \nu_2 }$. That is because
\begin{align} D_2 \in {\cal B}_{\Omega_2}, \; \; \nu_2 ( D_2 ) = 0 \quad \Longrightarrow \quad \nu_1 ( \phi_{1,2}^{-1} ( D_2 )) = 0 \quad \Longrightarrow \quad \mu_2 ( D_2 ) = 0 \tag{10.12} \end{align}Thus, by the Radon-Nikodym theorem, we get a continuous linear operator $[{\Phi}_{1,2}]_\ast :L^{1} (\Omega_1, \nu_1) \to L^{1} (\Omega_2, \nu_2)$.
Let ${\Phi}_{1,2}:L^\infty (\Omega_2) \to L^\infty (\Omega_1) $ be a deterministic causal operator. Then, it holds that
\begin{align} {\Phi}_{1,2} (f_2 \cdot g_2 ) = {\Phi}_{1,2} (f_2 ) \cdot {\Phi}_{1,2} (g_2 ) \qquad (\forall f_2, \forall g_2 \in L^\infty (\Omega_2 )) \end{align}Proof Let $f_2$, $g_2$ be in $L^\infty (\Omega_2)$. Let $\phi_{1,2}:\Omega_1 \to \Omega_2$ be the deterministic causal map of the deterministic causal operator ${\Phi}_{1,2}$. Then, we see
\begin{align} & [{\Phi}_{1,2} (f_2 \cdot g_2 )] (\omega_1) = (f_2 \cdot g_2 )(\phi_{1,2}(\omega_1)) = f_2(\phi_{1,2}(\omega_1)) \cdot g_2(\phi_{1,2}(\omega_1)) \\ = & [{\Phi}_{1,2} (f_2 )] (\omega_1) \cdot [{\Phi}_{1,2} (g_2 )] (\omega_1) = [{\Phi}_{1,2} (f_2 ) \cdot {\Phi}_{1,2} (g_2 )] (\omega_1) \qquad (\forall \omega_1 \in \Omega_1) \end{align} This completes the theorem.