9.11: Equal probability}: Monty Hall problem [three prisoners problem]
By Theorem 9.18 (The principle of equal weight),
the above Problems 9.25 and 9.26
is respectively the same as Problems 9.23 and 9.24
in the case that $p_1=p_2=p_3=1/3$.
This section is extracted from
the following:
$(\sharp):$
S. Ishikawa;
The Final Solutions of Monty Hall Problem and Three Prisoners Problem
S. Ishikawa, "A Measurement Theoretical Foundation of Statistics,"
arXiv:1408.0963v1 [stat.OT] 2014
$\quad$
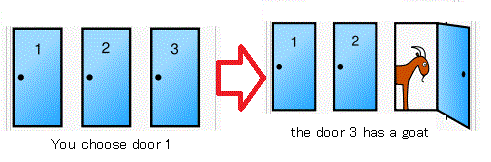
Suppose you are on a game show, and you are given
the choice of three doors
(i.e., " Door $A_1$"$\!\!\!,\;$ " Door $A_2$"$\!\!\!,\;$ " Door $A_3$"$\!\!)$.
Behind one door is a car, behind the others, goats.
You do not know what's behind the doors.
Thus,
$(\sharp_1):$
you select Door $A_1$
by the cast of the fair dice.
That is,
you say "Door $A_1$"
with probability
1/3.
The host,
who knows what's behind the doors, opens another door,
{say " Door $A_3$"$\!\!\!,\;$ which has a goat}.
He says to you,
" Do you want to pick Door $A_2$?"$\;\;$
Is it to your advantage to switch your choice of doors?
$\quad$
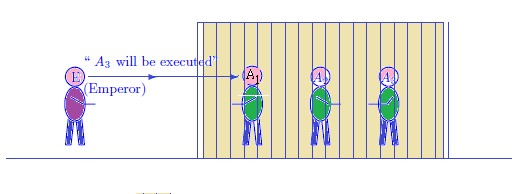
Three prisoners, $A_1$, $A_2$, and $A_3$ were in jail.
They knew that one of them was to be set free and
the other two were to be executed.
They did not know who was the one to be spared,
but the emperor did know.
Since three prisoners wanted to ask the emperor,
Then, $A_1$ said to the emperor,
"I already know that at least one the other two prisoners will be executed, so if you tell me the name of one who will be executed, you won't have given me any information about my own execution".$\;\;$
After some thinking, the emperor said,
"$A_3$ will be executed.}"$\;\;$
Thereupon $A_1$ felt happier because
his chance had increased from $\frac{1}{3(= {\rm Num}[\{A_1,A_2,A_3 \}])}$ to
$\frac{1}{2(= {\rm Num}[\{ A_1,A_2 \}])}$.
This prisoner $A_1$'s happiness may or may not be reasonable?
$(\sharp_2):$
the questioner was decided by the fair die throw.
And Prisoner $A_1$ was selected
with probability
$1/3$
Answer
$(B_1):$
Problem9.25
[Monty Hall problem ( the case that you throw a fair dice)]
\begin{align}
&
\mbox{
$\nu_{ post} (\{ \omega_1 \})$
$<$
$\nu_{ post} (\{ \omega_2 \})$
(i.e., $p_1=1/3 < 2/3=2 p_2 $),}
\\
&
\mbox{
thus, you should choose the door
$A_2$}
\end{align}
$(B_2):$ Problem9.26[three prisoners problem
( the case that the emperor throws a fair dice)],
\begin{align}
&
\mbox{
$
\nu_{0} (\{\omega_1\})
=
\nu_{\rm post} (\{\omega_1\})$
(i.e., $p_1 =1/3= 1- 2 p_2$),}
\\
&
\mbox{
Thus, the happiness of the prisoner $A_1$
is invariant}
\end{align}
$\fbox{Note 9.6}$
These problems
(i.e.,
Monty Hall problem
and the three prisoners problem)
continued attracting the philosopher's interest.
This is not due to
that
these are easy to make a mistake
for high school students,
but
9.11: Equal probability: Monty Hall problem [three prisoners problem]
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
Problem 9.25 [(=Problem9.16) Monty Hall problem(the casethat you throws the dice)]
Problem 9.26[three prisoners problem( the case that the prisoner throws the dice)]
