9.7: Monty Hall problem (The principle of equal weight)
9.7.1: The principle of equal weight--- The most famous unsolved problem
Let us reconsider
Monty Hall problem (Problem 9.14, Problem9.15)
in what follows.
We think that
the following is one of the most reasonable answers
(also, see Problem 19.5).
According to the rule ($\sharp$), you pick a door, say number 1, and the host,
who knows where the car is,
opens another door,
behind which is a goat.
For example,
the host says that
He says to you,
"Do you want to pick door number 2?"
Is it to your advantage to switch your choice of doors?
Answer
By the same way of Problem9.15
and
Problem9.16
(Monty Hall problem),
define
the
state space $\Omega = \{ \omega_1 , \omega_2 , \omega_3 \}$
and the
observable
${\mathsf O}=(X, {\cal F}, F)$.
And the observable
${\mathsf O}=(X, {\cal F}, F)$
is defined by
the formula
(9.11).
The map
$\phi:\Omega \to \Omega $
is defined by
we get a causal operator
$\Phi:L^\infty (\Omega) \to L^\infty(\Omega)$
by
$[\Phi(f)](\omega)
=
f(\phi(\omega))$
$(\forall f \in L^\infty(\Omega), \;\forall \omega \in \Omega )$.
Assume that
a car is behind the door $k$
$(k=1,2,3)$.
Then, we say that
We,
by the argument in Chapter 11 (cf. the formula (11.7))
see the following identifications:
Thus,
the above (a)
is equal to
Here, note that
$\frac{1}{3}(\delta_{\omega_k}+\delta_{\phi(\omega_k)}
+\delta_{\phi^2 (\omega_k)})$
$=$
$\frac{1}{3}(\delta_{\omega_1}+\delta_{\omega_2}
+\delta_{\omega_3})$
$(\forall k=1,2,3)$.
Thus,
this (b)
is identified with
the mixed measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}, S_{[{}\ast{}]}(\nu_e ))$
,
where
Therefore,
Problem 9.17
is the same as
Problem 9.16.
Hence,
you should choose
the door 2.
From the above argument,
we have the following theorem.
Theorem 9.18 [The principle of equal weight]
Consider a finite state space $\Omega$,
that is,
$\Omega=\{\omega_1,\omega_2,\ldots,\omega_n\}$.
Let
${\mathsf O}=(X, {\cal F}, F)$
be an observable in
$L^\infty (\Omega, \nu)$,
where $\nu$
is the counting measure.
Consider a measurement
$
{\mathsf M}_{L^\infty (\Omega )}({\mathsf O} ,
S_{[
\ast]}
)
$.
If the observer has no information for the state
$[\ast]$,
there is a reason to
that
this measurement is identified with
the mixed measurement
$
{\mathsf M}_{L^\infty (\Omega )}({\mathsf O} ,
{\overline S}_{[
\ast]}(w_e)
)
$
$\Big($
or,
$
{\mathsf M}_{L^\infty (\Omega )}({\mathsf O} ,
S_{[
\ast]}(\nu_e)
)
$
$\Big)$,
where
Proof.
The proof is a easy consequence of the above
Monty Hall problem
(or,
see
Problem 9.17 [Monty Hall problem(The principle of equal weight)]
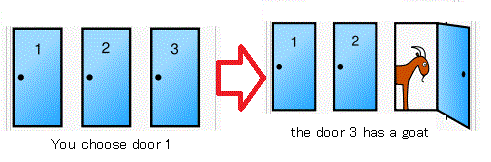
$\quad$
Suppose you are on a game show, and you are given
the choice of three doors
(i.e., "number 1"$\!\!\!,\;$ "number 2"$\!\!\!,\;$ "number 3"$\!\!)$.
Behind one door is a car, behind the others, goats.
$(\sharp):$
You choose a door
by the cast of the fair dice,
i.e.,
with probability
$1/3$.
$(\flat):$ the door 3 has a goat.
$(a):$
By the dice-throwing,
you get
$
\left[\begin{array}{ll}
1,2
\\
3,4
\\
5,6
\end{array}\right],
\mbox{then, take a measurement}
\left[\begin{array}{ll}
{\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}, S_{[{}\omega_k{}]})
\\
{\mathsf M}_{L^\infty (\Omega)} (\Phi{\mathsf O}, S_{[{}\omega_k{}]})
\\
{\mathsf M}_{L^\infty (\Omega)} (\Phi^2{\mathsf O}, S_{[{}\omega_k{}]})
\end{array}\right]
$
$(b):$ By the dice-throwing,
you get
$
\left[\begin{array}{ll}
1,2
\\
3,4
\\
5,6
\end{array}\right]
\mbox{then, take a measurement}
\left[\begin{array}{ll}
{\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}, S_{[{}\omega_k{}]})
\\
{\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}, S_{[{}\phi (\omega_k){}]})
\\
{\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}, S_{[{}\phi^2(\omega_k){}]})
\end{array}\right]
$
$\fbox{Note 9.4}$ The above argument is easy.
That is,
since you have no information,
we choose the door by a fair dice throwing.
In this sense,
the principle of equal weight
---
unless we have sufficient reason to regard one possible case
as more probable than another,
we treat them as equally probable
---
is clear in measurement theory.
However,
it should be noted that
the above argument is based on dualism.

).
$(\sharp):$
S. Ishikawa, "A Measurement Theoretical Foundation of Statistics,"
Applied Mathematics, Vol. 3, No. 3, 2012, pp. 283-292
$\fbox{Note 9.5}$ In this book, we deal with three
"the principle of equal weight" as follows:
$(\sharp_1):$
"the principle of equal weight" in Remark 5.19 ($\S$5.6)
$(\sharp_2):$
"the principle of equal weight" in Theorem 9.18 ($\S$9.7)
$(\sharp_3):$
"the principle of equal weight" in Proclaim 18.4 ($\S$18.2)
9.7:Monty Hall problem ( The principle of equal weight )
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
