Answer by Fisher's maximum likelihood method in $\S$5.5
Put
$\Omega = \{ \omega_1 , \omega_2 , \omega_3 \}$
with the discrete topology $d_D$ and the counting measure $\nu$.
Thus consider the classical basic structure:
Assume that
each state
$\delta_{\omega_m}
(\in
{\frak S}^p (C_0 (\Omega)^* ))$
means
Define the observable
${\mathsf O}_1$
$\equiv$
$(\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F_1)$
in $L^\infty (\Omega)$
such that
where
it is also possible to assume that
$F_1(\{ 2 \})(\omega_1)=\alpha$,
$F_1(\{ 3 \})(\omega_1) =1- \alpha$
$
(0 < \alpha < 1)$.
The fact that
you say
"the door 1"
means
that
we have a measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$.
Here, we assume that
Since the host said
"Door 3 has a goat"$\!\!\!,\;$
this implies that
you get the measured value "3"
by the measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[\ast]})$.
Therefore,
Theorem 5.6
(Fisher's maximum likelihood method)
says that
9.6: Monty Hall problem (The Bayesian approach)
9.6.1: The review of Problem5.14
(
Monty Hall problem in pure measurement)
$\quad$
You are on a game show and you are given the choice of three doors.
Behind one door is a car, and behind the other two are goats.
You choose, say, door 1, and the host, who knows where the car is,
opens another door,
behind which is a goat.
For example,
the host says that
And further,
He now gives you the choice of
sticking with door 1 or switching to door 2?
$(\flat):$
the door 3 has a goat.
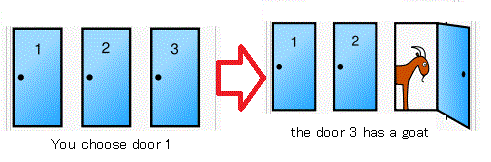
$(a):$
"a measured value $1$ is obtained"
$
\Leftrightarrow \mbox{The host says "Door 1
has a goat}$
(b):
"measured value $2$ is obtained"
$
\Leftrightarrow \mbox{The host says "Door 2
has a goat}$
(c):
"measured value $3$ is obtained"
$
\Leftrightarrow \mbox{The host says "Door 3
has a goat}$
That is because we see that
\begin{align} \max \{ [F_1(\{3\})] (\omega_1), [F_1(\{3 \}){}](\omega_2), [F_1(\{3 \})] (\omega_3) \} & =\max \{ 0.5, \; \; 1.0 , \; \; 0.0 \} \\ & =1.0 = [F_1(\{3\})] (\omega_2) \end{align}
and thus, there is a reason to infer that $[\ast]$ $=$ $\delta_{\omega_2}$. Thus, you should switch to door 2. This is the first answer to Monty-Hall problem.
Next, let us study Monty Hall problem in mixed measurement theory (particularly, Bayesian statistics).
Problem 9.16 [Monty Hall problem (The answer by Bayes' method)]

| $\quad$ | Suppose you are on a game show, and you are given
the choice of three doors
(i.e., "number 1"$\!\!\!,\;$ "number 2"$\!\!\!,\;$ "number 3"$\!\!)$.
Behind one door is a car, behind the others, goats.
You pick a door, say number 1.
Then,
the host,
who set a car behind a certain door,
says
And further, the host says, for example,
|
Answer In the same way as we did in Problem 9.15 (Monty Hall problem: the answer by Fisher's maximum likelihood method), consider the state space $\Omega = \{ \omega_1 , \omega_2 , \omega_3 \}$ with the discrete metric $d_D$ and the observable ${\mathsf O}_1$. Under the hypothesis ($\sharp_1)$, define the mixed state $\nu_0$ $(\in {\cal M}_{+1} (\Omega))$ such that
\begin{align} \nu_0= p_1 \delta_{\omega_1} + p_2 \delta_{\omega_2}+p_3 \delta_{\omega_3} \end{align} namely, \begin{align} \nu_0 (\{ \omega_1 \}) = p_1, \quad \nu_0 (\{ \omega_2 \}) = p_2, \quad \nu_0 (\{ \omega_3 \}) = p_3 \end{align}Thus we have a mixed measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]} ( \nu_0))$. Note that
| $a):$ |
"measured value $1$ is obtained
by the mixed measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1,
S_{[{}\ast{}]} ( \nu_0))$"
$ \Leftrightarrow \mbox{the host says "Door 1 has a goat"} $ |
| b): |
"measured value $2$ is obtained
by the mixed measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1,
S_{[{}\ast{}]} ( \nu_0))$"
$ \Leftrightarrow \mbox{the host says "Door 2 has a goat"} $ |
| c): |
"measured value $3$ is obtained
by the mixed measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1,
S_{[{}\ast{}]} ( \nu_0))$"
$ \Leftrightarrow $ the host says "Door 3 has a goat" |
Here, assume that, by the mixed measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]} (\nu_0))$, you obtain a measured value $3$, which corresponds to the fact that the host said "Door 3 has a goat"$\!\!\!.\;$ Then, Theorem 9.11 (Bayes' theorem) says that the posterior state $\nu_{ post}$ $(\in {\cal M}_{+1} (\Omega))$ is given by
\begin{align} \nu_{ post} = \frac{F_1(\{3\}) \times \nu_0} {\bigl\langle \nu_0, F_1(\{3\}) \bigr\rangle}. \end{align}That is,
\begin{align} & \nu_{ post} (\{ \omega_1 \})= \frac{\frac{p_1}{2}}{ \frac{p_1}{2} + p_2 }, \quad \nu_{ post} (\{ \omega_2 \})= \frac{p_2}{ \frac{p_1}{2} + p_2 }, \quad \nu_{ post} (\{ \omega_3 \}) = 0. \end{align}Particularly, we see that
| $(\sharp):$ | if $p_1 = p_2 = p_3 = 1/3$, then it holds that $\nu_{ post} (\{ \omega_1 \})=1/3$, $\nu_{ post} (\{ \omega_2 \})=2/3$, $\nu_{ post} (\{ \omega_3 \})=0$, and thus, you should pick Door 2. |
| $\fbox{Note 9.3}$ | It is not natural to assume the rule ($\sharp_1$) in Problem 9.16. That is because the host may intentionally set the car behind a certain door. Thus we think that Problem 9.16 is temporary. For our formal assertion, see Problem 9.17 latter and $\S$18.2 |
