EPR's paper:
(in $\S$4.4):
Concerning EPR's paper,
we shall add some remark as follows.
Let $A$ and $B$ be particles with the same masses $m$.
Consider the situation described in the following
figure:
can can do the various way to read.
Although its conclusion is not necessarily clear, but suggestive.
This will be shown as follows.
$\bullet$
Einstein, A., Podolosky, B. and Rosen, N.:
"Can quantum-mechanical description of reality
be considered completely?"
Physical Review Ser 2(47),
777--780,
(1935)
8.7 Syllogism does not hold in quantum systems
Remark 8.15 [Syllogism does not hold in quantum system]
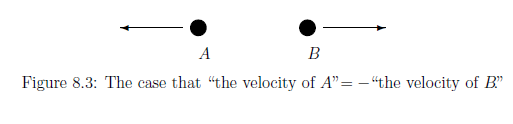
The position $q_A$ (at time $t_0$) of the particle A can be exactly measured, and moreover, the velocity of $v_B$ (at time $t_0$) of the particle B can be exactly measured. Thus, we may conclude that
| $(A):$ | the position and momentum (at time $t_0$) of the particle A are respectively and exactly equal to $q_A$ and $- m v_B$ ? |
(As mentioned in Section 4.3.3, this is not in contradiction with
Heisenberg' uncertainty principle).
However, we have the following question:
\begin{align} \Large{\mbox{Is the conclusion (A) true?}} \end{align}Now we shall describe the above arguments in quantum system:
A quantum two particles system $S$ is formulated in a tensor Hilbert space $H =H_1 \otimes H_1 = L^2 ({\mathbb R}_{q_1}) \otimes L^2 ({\mathbb R}_{q_2{}}) = L^2 ({\mathbb R}^2_{(q_1 , q_2)})$. The state ${u_0}$ $(\in H =H_1 \otimes H_1 = L^2 ({\mathbb R}^2_{(q_1 , q_2)}))$ $\Big($ or precisely, $\rho_0=| {u_0} \rangle \langle {u_0} | $ $\Big)$of the system $S$ is assumed to be
\begin{align} {u_0} (q_1 , q_2) = \sqrt{ \frac{1}{{{ 2 \pi \epsilon \sigma} }}} e^{ - \frac{1}{8 \sigma^2 } ({q_1 - q_2} - 2{a} )^2 - \frac{1}{8 \epsilon^2 } ({q_1 + q_2} )^2 } \tag{8.18} \end{align}where a positive number $\epsilon$ is sufficiently small. For each $k=1,2$, define the self-adjoint operators $Q_k{}\! : L^2 ({\mathbb R}^2_{(q_1 , q_2)}) \to $ $L^2 ({\mathbb R}^2_{(q_1 , q_2)}) $ and $P_k \!: L^2 ({\mathbb R}^2_{(q_1 , q_2)}) \to $ $L^2 ({\mathbb R}^2_{(q_1 , q_2)})$ by
\begin{align} & Q_1 = q_1 , \qquad P_1 = \frac{ \hbar \partial }{ i \partial q_1 } \nonumber \\ & Q_2 = q_2 , \qquad P_2 = \frac{ \hbar \partial }{ i \partial q_2 } \tag{8.19} \end{align}| $(\sharp_1):$ | Let ${\mathsf O}_1=({\mathbb R}^3, {\mathcal B}_{{\mathbb R}^3},F_1)$ be the observable representation of the self-adjoint operator $(Q_1 \otimes P_2 ) \times (I \otimes P_2 )$. And consider the measurement ${\mathsf M}_{B(H)} ({\mathsf O}_1=({\mathbb R}^3, {\mathcal B}_{{\mathbb R}^3},F_1), S_{[|u_0 \rangle \langle u_0|]})$. Assume that the measured value $(x_1, p_2, p_2 ) (\in {\mathbb R}^3 )$. That is, \begin{align} \underset{\mbox{ (the position of $A_1$, the momentum of $A_2$)}}{(x_1, p_2)} \;\; \underset{{\mathsf M}_{B(H)}({\mathsf O}_1,S_{[\rho_0]})}{\Longrightarrow} \;\; \underset{\mbox{ the momentum of $A_2$}}{p_2} \end{align} |
| $(\sharp_2):$ | Let ${\mathsf O}_2=({\mathbb R}^2, {\mathcal B}_{{\mathbb R}^2},F_2)$ be the observable representation of $(I \otimes P_2 ) \times (P_1 \otimes I )$. And consider the measurement ${\mathsf M}_{B(H)} ({\mathsf O}_2=({\mathbb R}^2, {\mathcal B}_{{\mathbb R}^2},F_2), S_{[|u_0 \rangle \langle u_0|]})$. Assume that the measured value $(p_2, -p_2 ) (\in {\mathbb R}^3 )$. That is, \begin{align} \underset{\mbox{ the momentum of $A_2$}}{p_2} \;\; \underset{{\mathsf M}_{B(H)}({\mathsf O}_2,S_{[\rho_0]})}{\Longrightarrow}\;\; \underset{\mbox{ the momentum of $A_1$}}{- p_2} \end{align} |
| $(\sharp_3):$ | Therefore, by $(\sharp_1)$ and $(\sharp_2)$, "syllogism" may say that \begin{align} \underset{\mbox{ the momentum of $A_1$}}{- p_2} \qquad \Big(\mbox{ that is, the momentum of $A_1$ is equal to $-p_2$} \Big) \end{align} |
| $(B):$ | $\color{blue}{{\mbox{The (A) is true}}}$ |
| $(\sharp_4):$ | $
(Q_1 \otimes P_2 ) \times (I \otimes P_2 )
$
and
$(I \otimes P_2 ) \times (P_1 \otimes I )$
(
Therefore,
${\mathsf O}_1$
and
${\mathsf O}_2$
)
do not commute,
and thus,
the simultaneous observable does not exist.
Thus, we can not test the $(\sharp_3)$ experimentally. |
| $(C_1):$ | syllogism does not hold in quantum systems, |
| $(C_2):$ | there is something faster than light |
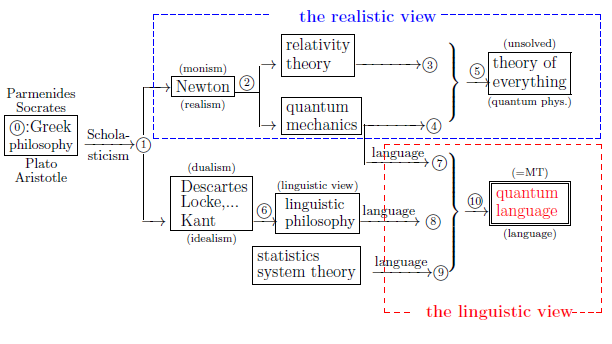 |
| $\qquad \quad $ Fig.1.1: The history of world-descriptions |
We think that the (C$_1$) is not serious. Thus, we do not need to investigate how to understand the fact (C$_1$). On the other hand, the (C$_2$) is seroius. Although we have to effort to understand the "fact (C$_2$)", this is the problem in physics (i.e., in ⑤ in Figure 1.1). Recall that the spirit of quantum language (i.e., in ⑩ in Figure 1.1) is
