5.5: Manty Hall problem: non-Baysian approach
Put $\Omega = \{ \omega_1 , \omega_2 , \omega_3 \}$ with the discrete topology $d_D$ and the counting measure $\nu$. Thus consider the classical basic structure:
Define the observable ${\mathsf O}_1$ $\equiv$ $(\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F_1)$ in $L^\infty (\Omega)$ such that
where it is also possible to assume that $F_1(\{ 2 \})(\omega_1)=\alpha$, $F_1(\{ 3 \})(\omega_1) =1- \alpha$ $
(0 < \alpha < 1)$. The fact that you say "the door 1" clearly means that you take a measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$.
Here, we assume that
Recall that, in Problem 5.14, the host said "Door 3 has a goat"$\!\!\!.\;$ This implies that you get the measured value "3" by the measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[\ast]})$. Therefore, Theorem 5.6
(Fisher's maximum likelihood method) says that
and thus, there is a reason to infer that the unknown state $ [\ast]$ is equal to $\delta_{\omega_2}$. Thus,
you should switch to door 2. This is the first answer to Problem 5.14 (Monty-Hall problem).
Also, for a Bayesian approach to Monty Hall problem, see Chapter 9 and Chapter 19.
In the above, a measured value "3" is obtained by the measurement ${\mathsf M}_{L^\infty (\Omega )} ({\mathsf O} {{=}}(\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F),$ $ S_{[{}\ast{}]})$. Thus, the approximate sample space $(\{1,2,3\}, 2^{\{1,2,3\}}, \nu_{1})$
is obtained such that $\nu_1 (\{1 \}) =0 $, $\nu_1 (\{2 \}) =0 $, $\nu_1 (\{3 \}) =1 $. Therefore,
Thus, we can infer that $[\ast]$ $=$ ${\omega_2}$. That is, you should change to the Door 2.
And further, he now gives you the choice of sticking with door 1 or switching to door 2? What should you do?
$(\flat):$ the door 3 has a goat. 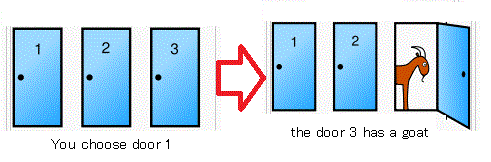
(a): "a measured value $1$ is obtained by the measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$"
$
\Leftrightarrow \mbox{The host says "Door 1
has a goat"}$ (b): "measured value $2$ is obtained by the measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$"
$
\Leftrightarrow \mbox{The host says "Door 2
has a goat"}$ (c): "measured value $3$ is obtained by the measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$"
$
\Leftrightarrow \mbox{The host says "Door 3
has a goat"}$
Remark 5.15 [The answer by the moment method]
$\fbox{Note 5.4}$ Examining the above example, the readers should understand that the problem "What is measurement?" is an unreasonable demand. Thus,
\begin{align}
\mbox{
we have to abandon the realistic approach,
and accept
the metaphysical approach.
}
\end{align}
In other words, we assert that
\begin{align}
\mbox{
the concept of measurement is metaphysical.
}
\end{align}
5.5: Manty Hall problem by Fisher's maximum likelihood method
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
Problem 5.14 [Monty Hall problem]
You are on a game show and you are given the choice of three doors. Behind one door is a car, and behind the other two are goats. You choose, say, door 1, and the host, who knows where the car is, opens another door, behind which is a goat. For example, the host says that
Figure 5.8 Monty Hall prroblem
Answer:
