Contents:

2.4.1 Dualism (John Locke)

Our present purpose is to learnAxiom 1 ( measurement ) by rote The "learning by rote" urges us to understand the mathematical definitions of
$(\sharp_1):$Basic structure$[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$, state space ${\frak S}^p({\cal A}^*)$
$(\sharp_2):$observable ${\mathsf O}{{=}} (X, {\cal F} , F{})$, etc.

In the previous section, we studied the above $(\sharp_1)$, that is, we discussed the following classification:

(B): $\underset{\mbox{ state space }[{\frak S}^p({\cal A}^*),{\frak S}^m({\cal A}^*),\overline{\frak S}^p(\overline{\cal A}_*)]}{\mbox{General basic structure}[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}}$ $\quad \qquad \Longrightarrow \left\{\begin{array}{ll} \underset{\mbox{ state space }[{\frak S}^p({\mathcal Tr}(H)),{\frak S}^m({\mathcal Tr}(H))= \overline{\frak S}^m({\mathcal Tr}(H))]}{\mbox{Quantum basic structure}[ {\mathcal C}(H) \subseteq B(H)]_{B(H)}} \\ \\ \\ \underset{\mbox{ state space }[\Omega, {\mathcal M}_{+1}(\Omega),L^\infty(\Omega, \nu ) ]}{\mbox{Classical basic structure}[ C_0(\Omega) \subseteq L^\infty(\Omega, \nu )]_{B(L^2(\Omega, \nu ))}} \end{array}\right. $

In this section, we shall study the above $(\sharp_2)$, i.e.,



$ \mbox{ "Observable" } $


Recall the famous words: "the primary quality"and "the secondary quality" due to John Locke,an English philosopher and physician regarded as one of the most influential of Enlightenment thinkers and known as the "Father of British empiricism". We think the following correspondence: \begin{align} \left\{\begin{array}{ll} \mbox{[state]} & \longleftrightarrow \mbox{[the primary quality]} \\ \mbox{[observable]} & \longleftrightarrow \mbox{[the secondary quality]} \end{array}\right. \tag{2.47} \end{align} And thus, we think

$\bullet$:These (i.e.,"state" and "observable") are the concepts which form the basis of dualism.

Also, the following table promotes the better understanding of quantum language as well as the other world-views(i.e., the conventional philosophies).


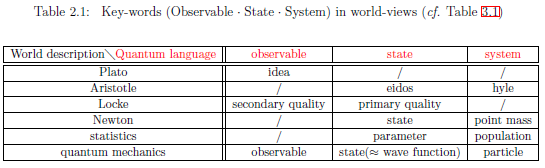
Although I am not familiar with "ontology", I want to consider that "key-word" exists in each world-view



$\fbox{Note 2.2}$ It may be understandable to consider \begin{align} \mbox{ "observable" ="the partition of word"="the secondary quality" } \end{align}



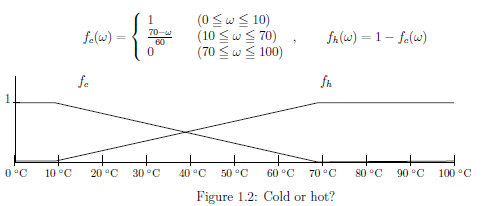
For example, Chapter 1 (Figure 1.2) says that $\big( f_{{c}}, f_{{h}} \big)$ is the partition between "cold" and "hot". Also, "measuring instrument" is the instrument that choose a word among words. In this sense, we consider that "observable"= "measuring instrument". Also, The reason that John Locke's sayings "primary quality (e.g., length, weight, etc.)" and "secondary quality (e.g., sweet, dark, cold, etc.)" is that these words form the basis of dualism.

2.4.2 Dualism (in philosophy) and duality (in mathematics)

The following question may be significant:

(C1): Why did philosophers continue persisting in dualism?


As the typical answer, we may consider that

(C2): "I" is the special existence, and thus, we would like to draw a line between "I" and "matter".


But, we think that this is only quibbling. We want to connect the question (C$_1$) with the following mathematical question:

(C3): Why do mathematicians investigate "dual space"?


Of course, the question "why?" is non-sense in mathematics. If we have to answer this, we have no answer except the following (D):

(D): If we consider the dual space ${\mathcal A}^*$, calculation progresses deeply.


Thus, we want to consider the relation between the dualism and the dual space such as \begin{align} \left\{\begin{array}{ll} \mbox{[the primary quality]} & \longleftrightarrow \mbox{the state in the dual space ${\mathcal A}^*$} \\ \mbox{[the secondary quality]} & \longleftrightarrow \mbox{the observable in $C^*$ algebra ${\mathcal A}$ (or, $W^*$-algebra $\overline{\mathcal A}$)} \end{array}\right. \end{align} Hence, we consider that the answer to the (C$_1$) is also
"calculation progresses deeply"
or
"power of expression increases".

2.4.3 Essentially continuous

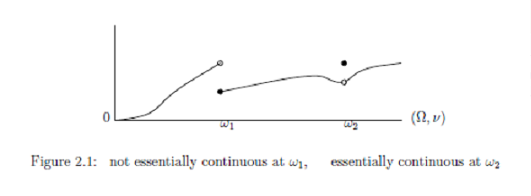
In $\S$2.1..2, we introduced the following diagram:
(E):General basic structure and state space \begin{align} & \begin{array}{rlrlll} \underset{C^*-pure state}{{\frak S}^p({\mathcal A}^*)} \subset \underset{{\mbox{ $C^*$-mixed state}}}{{\frak S}^m({\mathcal A}^*)} \subset & {\mathcal A}^* &&&& \\ & \Big\uparrow \mbox{ dual} &&&& \\ & \fbox{$ {\mathcal A}$} & \xrightarrow[\mbox{ subalgebra$\cdot$weak-closure}]{\subseteq} & \fbox{${\overline{\mathcal A}}$} & \xrightarrow[\mbox{ subalgebra}]{\subseteq} \fbox{${B(H)}$} & \\ & && \quad \Big\downarrow \;\mbox{ pre-dual} && \end{array} \tag{2.50} \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \underset{{\mbox{ $W^*$-mixed state}}}{\overline{\frak S}^m(\overline{\mathcal A}_*)} \subset \overline{\mathcal A}_* \nonumber \end{align}
In the above diagram, we introduce the following definition.
Definition 2.14 [Essentially continuous] An element $F (\in \overline{\cal A} )$ is said to be essentially continuous at $\rho_0 (\in {\frak S}^m ({}{\cal A}^*{}))$, if there uniquely exists a complex number $\alpha$ such that
(F1): if $\rho_n　( \in {\overline{\frak S}^m(\overline{\mathcal A}_*)})$ weakly converges to　$\rho_0 (\in {\frak S}^m ({}{\cal A}^*{}))$. That is, $$　\lim_{n \to \infty } {}_{\overline{\mathcal A}_\ast} \Big( \rho_n, G \Big){}_{{\mathcal A}}　= {}_{{\mathcal A}^\ast} \Big( \rho_0, G \Big){}_{{\mathcal A}} (\forall G \in {\cal A} (\subseteq \overline{\cal A} ) ), $$ then it holds that $$ \lim_{n \to \infty } {}_{\overline{\mathcal A}_\ast} \Big( \rho_n, F \Big){}_{\overline{\mathcal A}} =\alpha $$
Then, the value $\rho_0(F) ( = {}_{{\mathcal A}^\ast} \Big( \rho_0, F \Big){}_{\overline{\mathcal A}} )$ is defined by the $\alpha$.

Of course, for any $\rho_0 (\in {\frak S}^m ({}{\cal A}^*{}))$, $F (\in {\mathcal A})$ is essentially continuous at $\rho_0$. This "essentially continuous" is chiefly used in th case that $\rho_0 (\in {\frak S}^p ({}{\cal A}^*{}))$.


Remark 2.1 [Essentially continuous in quantum system and classical system] Consider the quantum basic structure $[{\mathcal C}(H) \subseteq B(H)]_{B(H)}$. Then, we see \begin{align*} ({\mathcal C}(H))^*= {\mathcal {\mathcal Tr}(H)} = B(H)_* \end{align*}

Thus, we haven $\rho \in {\frak S}^p({\mathcal C}(H)^*) \subseteq {\mathcal Tr}(H)$, $F \in \overline{{\mathcal C}(H)}=B(H)$, which implies that

\begin{align} \rho(G)= {}_{{\mathcal C}(H)^*} \Big( \rho, F )\Big){}_{B(H)} = {}_{{\mathcal Tr}(H)} \Big( \rho, F )\Big){}_{B(H)} \tag{2.51} \end{align} Thus, we see that "essentially continuous" $\Leftrightarrow$ "continuous" in quantum case.

[II]: Next, consider the classical basic structure $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$. A function $F$ $( \in L^\infty ( \Omega, \nu ))$ is essentially continuous at $\omega_0$ $( \in \Omega = {\frak S}^p(C_0(\Omega )^*) )$, if and only if it holds that

(F2): if $\rho_n (\in L_{+1}^1(\Omega, \nu )$ satisfies that \begin{align*} \lim_{n \to \infty } \int_\Omega G(\omega ) \rho_n(\omega) \nu (d \omega ) =G(\omega_0) \qquad (\forall G \in C_0(\Omega ) ) \end{align*} then there uniquely exists a complex number $\alpha$ such that \begin{align} \lim_{n \to \infty } \int_\Omega F(\omega) \rho_n (\omega) \nu (d \omega ) = \alpha \tag{2.52} \end{align}
Then, the value of $F(\omega)$ is defined by $\alpha$, that is, $F(\omega_0 )=\alpha$.

2.4.4 The definition of "observable (=measuring instrument)"

Definition 2.16 [Set ring,set field,$\sigma$-field]

Let $X$ be a set ( or locally compact space). The ${\cal F}\Big( \subseteq 2^X = {\mathcal P}(X)=\{ A \;|\; A \subseteq X \}, \mbox{the power set of $X$}\Big)$ (or, the pair $(X, {\mathcal F})$) is called a ring ( of sets), if it satisfies that

\begin{align*} & ({\rm a}): \emptyset (\mbox{="empty set"})\in {\cal F}, \quad \\ & ({\rm b}): \Xi_i \in {\cal F} \quad (i=1,2,\ldots) \Longrightarrow { \bigcup\limits_{i=1}^n } \;\; \Xi_i \in {\cal F} ,\quad { \bigcap\limits_{i=1}^n } \;\; \Xi_i \in {\cal F} \\ & ({\rm c}): \Xi_1 , \Xi_2 \in {\cal F} \Longrightarrow \Xi_1 \setminus \Xi_2 \in {\cal F} \quad (\mbox{ where, } \Xi_1 \setminus \Xi_2= \{ x \;| \; x \in \Xi_1 , x \notin \Xi_2 \}) \end{align*}

Also, if $X \in {\mathcal F}$ holds, the ring ${\mathcal F}$(or, the pair $(X, {\mathcal F})$) is called a field (of sets) And further,

(d): if the formula (b) holds in the case that $n=\infty$, a field ${\mathcal F}$ is said to be $\sigma$-field. And the pair $( X, {\mathcal F} )$ is called a measurable space.
The following definition is most important. In this note, we mainly devote ourselves to the $W^*$-observable.
Definition 2.17 [Observable,measured value space] Consider the basic structure \begin{align*} [{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)] \end{align*} (G$_1$):$C^*$- observable A triplet ${\mathsf{O}} {=} (X, {\cal R}, F)$ is called a $C^*$-observable (or, $C^*$-measuring instrument ) in ${\mathcal A}$, if it satisfies as follows.
$(i)$: $(X, {\mathcal R})$ is a ring of sets.
$(ii)$: a map $F: {\cal R} \to {\mathcal A}$ satisfies that
(a):　$0 {{\; \leqq \;}}F (\Xi) \le I$　$\quad( \forall \Xi \in {\mathcal R}) $,$F (\emptyset) = 0$,
(b):　for any $\rho ( \in {\frak S}^p({\mathcal A}^*) )$,　there exists a probability space　$(X, \overline{\mathcal R}, P_\rho )$　such that　(where,$\overline{\mathcal R}$ is the smallest $\sigma$-field such that 　${\mathcal R} \subseteq \overline{\mathcal R}$)　such that \begin{align} {}_{\stackrel{{}}{{\mathcal A}_* }}\Big(\rho, F(\Xi) \Big){}_{\stackrel{{}}{{\mathcal A} }} = P_\rho (\Xi ) \qquad (\forall \Xi \in {\mathcal R} ) \tag{2.53} \end{align}
Also, $X$ [resp. $(X, {\mathcal F}, P_\rho )$] is called a measured value space [resp. sample probability space ].
(G$_2$):$W^*$- observable A triplet ${\mathsf{O}} {=} (X, {\cal F}, F)$ is called a $W^*$-observable (or, $W^*$-measuring instrument ) in $\overline{\mathcal A}$, if it satisfies as follows.
$(i)$: $(X, {\mathcal F})$ is a $\sigma$-field.
$(ii)$:a map $F: {\cal F} \to \overline{\mathcal A}$ satisfies that
(a): $0 {{\; \leqq \;}}F (\Xi) $ $\quad( \forall \Xi \in {\mathcal F}) $, $F (\emptyset) = 0$, $F (X) = I$
(b): for any $\overline{\rho} ( \in \overline{\frak S}^m(\overline{\mathcal A}_*) )$, there exists a probability space $(X, {\mathcal F}, P_{\overline{\rho}} )$ such that \begin{align} {}_{\stackrel{{}}{\overline{\mathcal A}_* }}\Big(\overline{\rho}, F(\Xi) \Big){}_{\stackrel{{}}{\overline{\mathcal A} }} = P_{\overline{\rho}} (\Xi ) \qquad (\forall \Xi \in {\mathcal F} ) \tag{2.54} \end{align}
The observable ${\mathsf{O}} {=} (X, {\cal F}, F)$ is called a projective observable, if it holds that \begin{align*} F(\Xi)^2 = F(\Xi) \qquad (\forall \Xi \in {\mathcal F} ). \end{align*}
We assume the following definition:
Definition 2.18 Let $\rho \in {\frak S}^m({\mathcal A}^*) $, and $(X, {\mathcal F}, F )$ be a $W^*$-observable in $\overline{\mathcal A}$. ${\mathcal F}_\rho = \{ \Xi \in {\mathcal F} \;|\;$ $F(\Xi)$ is essentially continuos at $\rho$ $\}$. The probability space $(X, {\mathcal F}, P_\rho )$ is called its sample probability space , if it holds that
$(\sharp_1)$: ${\mathcal F}$ is the smallest $\sigma$-field that contains ${\mathcal F}_\rho$.
$(\sharp_2)$: \begin{align} {}_{\stackrel{{}}{{\mathcal A}^* }}\Big(\rho, F(\Xi) \Big){}_{\stackrel{{}}{\overline{\mathcal A} }} = P_\rho (\Xi ) \qquad (\forall \Xi \in {\mathcal F}_\rho ) \end{align}

Concerning the $C^*$-observable, the sample probability space clearly exists. On the other hand, concerning the $W^*$-observable, we have to say something as follows. As mentioned in Remark 2.15, in quantum cases ( thus, ${\mathcal A}^*= {\mathcal Tr}(H)=\overline{\mathcal A}_*$ ), the ($\sharp_1$) and ($\sharp_2$) clearly hold. However, in the classical cases, we do not know whether the existence of the sample probability space follows from the definition of the $W^*$-observable. Thus, in this book, we do not add the condition ($\sharp$) in the definition of the $W^*$-observable.

In this book, we always assume the following hypothesis:
Hypothesis 2.19 [Sample probability space] In the above situation, the existence of the sample probability space is always assumed.