Let ${\mathbb C}$ be the set of all complex numbers.
Let $H$ be a complex Hilbert space with a inner product $\langle \cdot , \cdot \rangle $, where the inner product
$\langle \cdot , \cdot \rangle : H \times H \to {\mathbb C} $ satisfies that
And, defining the norm $\| u \| $ (or $\|u \|_H $) by $\| u \| =| \langle u , u \rangle|^{1/2} $, we get the Banach space $(H, \| \cdot \|)$. Define $B(H)$ by
$B(H)$ is regarded as the Banach space with the operator norm $\| \cdot \|_{B(H)}$,
Let $T \in B(H)$. The dual operator $T^* \in B(H)$ of $T$ is defined by
Furthermore, the following equality (called the
"$C^*$-condition"
) holds:
When $T=T^*$ holds, $T$ is called a self-adjoint operator (or, Hermitian operator). Let $T_n (n \in {\mathbb N} =\{ 1,2, \cdots\} ),T \in B(H)$. The sequence $\{T_n \}_{n=1}^\infty $ is said to converge in the sense of the (operator) norm topology to $T$ (that is, $n-\lim_{n \to \infty } T_n = T$), if
Also, the sequence $\{T_n \}_{n=1}^\infty $ is said to converge weakly to $T$ (that is, $w-\lim_{n \to \infty } T_n = T$ ), if
Thus, we have two convergences (i.e., norm convergence and weakly convergence) in $B(H)$.
The concept of "state space" is fundamental in quantum language. This is formulated in the dual space ${\mathcal A}^*$ of $C^*$-algebra ${\mathcal A}$ (or, in the pre-dual space $\overline{\mathcal A}_*$ of $W^*$-algebra $\overline{\mathcal A}$).
Assume that $\overline{\mathcal A}_*$ is the pre-dual space of $\overline{\mathcal A}$. Then, another mixed state space $\overline{\frak S}^m(\overline{\mathcal A}_*)$ is defined by
That is, we have two "mixed state spaces", that is, $C^*$-mixed state space ${\frak S}^m({\mathcal A}^*)$
and $W^*$-mixed state space $\overline{\frak S}^m({\overline{\mathcal A}}_*)$.
Contents

2.1.1:Hilbert space and operator algebra
$\bullet$ ${\langle w, w \rangle} \ge 0 \; (\forall w \in H )$,
$\qquad$
$\quad$
$\bullet$ ${\langle w, w \rangle}=0 \Leftrightarrow w=0$,
$\bullet$ ${\langle w, \alpha_1 w_1 + \alpha_2 w_2 \rangle} = \alpha_1 {\langle w, w_1 \rangle}+ \alpha_2 {\langle w, w_2 \rangle} \quad (\forall w, w_1, w_2 \in H,
\forall \alpha_1, \alpha_2 \in {\mathbb C})$,
$\bullet$ ${\langle w_1, w_2 \rangle} = \overline{\langle w_2, w_1 \rangle}$ (i.e.,, conjugate complex) $(\forall w_1, w_2 \in H)$

 \begin{align*}
(T^*)^* =T, \quad
(T_1 T_2 )^* = T_2^* T_1^*
\end{align*}
\begin{align*}
(T^*)^* =T, \quad
(T_1 T_2 )^* = T_2^* T_1^*
\end{align*}
${\mathcal A} (\subseteq B(H) )$ is called a $C^*$-algebra, if it satisfies that
Also, a $C^*$-algebra${\mathcal A} (\subseteq B(H) )$ is called a $W^*$-algebra, if it is weak closed in $B(H)$.
$(A_1):$ ${\mathcal A} (\subseteq B(H) )$ is the closed linear space in the sense of the operator norm $\| \cdot \|_{B(H)}$.
$(A_2):$ ${\mathcal A}$ is $\ast$-algebra, that is, ${\mathcal A} (\subseteq B(H) )$ satisfies that
\begin{align*}
F_1, F_2 \in {\mathcal A} \Rightarrow F_1 \cdot F_2 \in {\mathcal A},
\qquad
F \in {\mathcal A} \Rightarrow F^* \in {\mathcal A}
\end{align*}
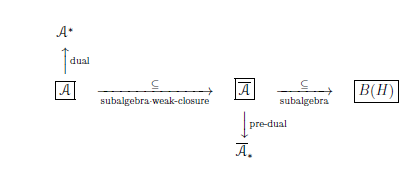
2.1.2 Basic structure$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$;$\;\;$ general theory
Consider the basic structure $[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ $\Big($ or, denoted by $[{\mathcal A} \subseteq \overline{\mathcal A}]_{ B(H)}$ $\Big)$.
That is,
(A): ${\mathcal A} ( \subseteq B(H))$ is a $C^*$-algebra, and $\overline{\mathcal A} ( \subseteq B(H))$ is the weak closure of ${\mathcal A}$.
Note that $W^*$-algebra $\overline{\mathcal A}$ has the pre-dual Banach space $\overline{\mathcal A}_*$( that is,
$(\overline{\mathcal A}_*)^*=\overline{\mathcal A}$) uniquely. Therefore, the basic structure$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ is represented as follows.
2.1.3: Basic structure$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ and state space;$\;\;$General theory
 Consider the basic structure:
\begin{align*}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align*}
Let ${\mathcal A}^*$ be the dual space of the $C^*$-algebra${\mathcal A}$. The mixed state space ${\frak S}^m({\mathcal A}^*)$ and the {pure state space ${\frak S}^p({\mathcal A}^*)$ is respectively defined by
Consider the basic structure:
\begin{align*}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align*}
Let ${\mathcal A}^*$ be the dual space of the $C^*$-algebra${\mathcal A}$. The mixed state space ${\frak S}^m({\mathcal A}^*)$ and the {pure state space ${\frak S}^p({\mathcal A}^*)$ is respectively defined by
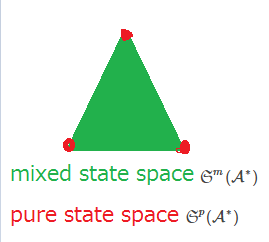
The mixed state space ${\frak S}^m({\mathcal A}^*)$ and the pure state space ${\frak S}^p({\mathcal A}^*)$
are locally compact spaces
(a): ${\frak S}^m({\mathcal A}^*)=\{ \rho \in {\mathcal A}^* \;| \; \|\rho \|_{{\mathcal A}^*}=1, \rho \ge 0 \mbox{ (i.e., $\rho(T^* T) \ge 0 (\forall T \in {\mathcal A})$)}\}$
(b): ${\frak S}^p({\mathcal A}^*)=\{ \rho \in {\frak S}^m({\mathcal A}^*) \; | \;
\rho \mbox{ is a pure state} \}$. Here, $\rho (\in {\frak S}^m({\mathcal A}^*))$ is a pure state if and only if
\begin{align*}
\rho = \alpha \rho_1 + (1-\alpha ) \rho_2, \;\; \rho_1 , \rho_2 \in {\frak S}^m({\mathcal A}^*), 0 < \alpha <1
\Longrightarrow \rho=\rho_1=\rho_2
\end{align*}
(c): $\overline{\frak S}^m({\overline{\mathcal A}}_*) =\{ \rho \in
{\overline{\mathcal A}}_* \;| \; \|\rho \|_{\overline{\mathcal A}_*}=1, \rho \ge 0 \mbox{ (i.e., $\rho(T^* T) \ge 0 (\forall T \in \overline{\mathcal A})$)}\}$
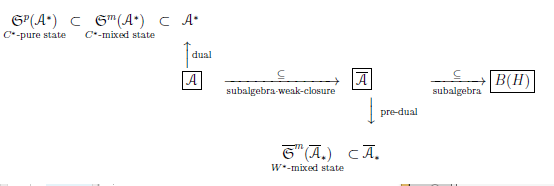
In this note, we mainly discuss Fisher statistics (i.e., $\mbox{pure state space:}{{\frak S}^p({\mathcal A}^*)}$). In the case case of Bayesian statistics, we chiefly devote ourselves to the $W^*$-mixed state${\overline{\frak S}^m(\overline{\mathcal A}_*)}$ rather than the $C^*$-mixed state} ${{\frak S}^m({\mathcal A}^*)}$, though the two play the similar roles in quantum language.
(D):
$
\left\{\begin{array}{ll}
\mbox{Fisher statistics} & \cdots \mbox{pure state space:}{{\frak S}^p({\mathcal A}^*)}
\color{blue}{\mbox{:
most fundamental
}}
\\
\\
\mbox{Bayes statistics} & \cdots
\left\{\begin{array}{ll}
\mbox{$C^*$-mixed state space:${{\frak S}^m({\mathcal A}^*)}$}
\color{blue}{\mbox{:
easy
}}
\\
\\
\mbox{$W^*$-mixed state space:${\overline{\frak S}^m(\overline{\mathcal A}_*)}$}
\color{blue}{\mbox{:
natural, useful
}}
\end{array}\right.
\end{array}\right.
$
2.1: Basic structure $[{\mathcal A} \subseteq$ $ \overline{\mathcal A} \subseteq B(H)]$( General Theory)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
Definition 2.1 [$C^*$-algebra and $W^*$-algebra]
Definition 2.2. [General basic structure:$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$]
General basic structure:$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$
Definition 2.3.[State space, mixed state space]
Remark2.4 In order to avoid the confusions, three "state spaces" should be explained in what follows.
